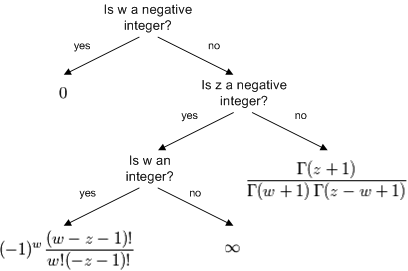
My previous post showed how to define binomial coefficients for general arguments. I just posted an article that explains how to compute binomial coefficients. Here’s a chart from the article for computing the binomial coefficient (z, w) for arbitrary complex z and w.
See also How to calculate binomial probabilities.

An interesting exercise is to calculate the exact number of trailing zeros in (n!) for large (n), such as (99!) or (1000!).
can someone explain to me why the use gamma of z or w plus one? Why can’tthey just do z! or w!? that would be so much easier, right?
Evan: There are historical reasons for the choice of definition of the gamma function. Gamma could have been defined so that for positive integers, Gamma(n) = n! instead of (n-1)!. Each choice of definition makes some formulas simpler and some more complicated. On balance, the standard definition simplifies more formulas than it complicates. At least that was the opinion of the people who standardized the definition, and I imagine a lot of people agree they made the right choice.
Here’s a nice mathoverflow discussion on the off-by-oneness of the gamma function.