Here’s something I do all the time. I have a function of one variable and several parameters. I implement it as a function object in C++ so I can pass it on to code that does something with functions of one variable, such as integration or optimization. I’ll give a trivial example and then show the most recent real problem I’ve worked on.
Say I have a function f(x; a, b, c) = 1000a + 100b + 10c + x. In a sense this is simply a function of four variables. But the connotation of using a semicolon rather than a comma after the x is that I think of x as being a variable and I think of a, b, and c as parameters. So f is a function of one variable that depends on three constants. (A “parameter” is a “constant” that can change!)
I create a C++ function object with two methods. One method is a constructor that takes the function parameters as arguments and saves them to member variables. The other method is an overload of the parenthesis method. That’s what makes the class a function object. By overloading the parenthesis method, I can call an instance of the class as if it were a function. Here’s some code.
class FunctionObject
{
public:
FunctionObject(double a, double b, double c)
{
m_a = a;
m_b = b;
m_c = c;
}
double operator()(double x) const
{
return 1000*m_a + 100*m_b + 10*m_c + x;
}
private:
double m_a;
double m_b;
double m_c;
};
So maybe I instantiate an instance of this function object and pass it to a function that finds the maximum value over an interval [a, b]. The code might look like this.
FunctionObject f(3, 1, 4); double maximum = Maximize(f, a, b);
Here’s a more realistic example. A few days ago I needed to solve this problem. Given user input parameters λ, σ, n, and ξ, find b such that the following holds.
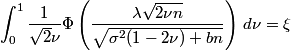
The function Φ above is the CDF of a standard normal random variable, defined here.
To solve this problem, I wrote a function object to evaluate the left side of the equation above. It takes λ, σ, and n as constructor arguments and takes b as an argument to operator(). Then I passed the function object to a root-finding method to solve for the value of b that makes the function value equal ξ. But my function is defined in terms of an integral, so I needed to write another function object first that returns the integrand. Then I pass that function object to this numerical integration routine. So I had to write two function objects to solve this problem.
There are several advantages to function objects over functions. For example, I would typically do parameter validation in the constructor. Quite often I also do some expensive calculations in the constructor and cache the results so that each call to operator() is then more efficient. Maybe I want to keep track of how often the function is called, so I put in some sort of odometer method that increments a counter with each call.
Unfortunately there’s a fair amount of code to write in order to implement even the simplest function. This effort hardly matters in production code; so many other things take more time. But it is annoying when doing some quick exploration. The next post shows how this can be done much easier in Python. The Python approach would be much easier for small problems, but it doesn’t have the advantages mentioned above such as caching expensive calculations in a constructor.

I would much rather prefer something like:
struct Function
{
double operator()(double a, double b, double c, double x)
{ return 1000 * a + 100 * b + 10*c + x; }
};
double maximum = Maximize(bind(Function(),3,1,4,_1),a,b)
For this example, it is kind of overkill but my general preference is to prefer free functions and boost bind to generate functions :-)
Sohail,
The problem with your approach is that the constants must be added to the stack every time f(x) is called (bind isn’t cheap to use.) If one is using a zero finder that uses reverse communication, using bind will add significant overhead to the call. By storing the constants internally in the structure, as in the original example, you trade more or less constant heap storage for very dynamic stack storage of the constants. I also like John’s approach because you don’t have to drag boost into the problem.
Sohail’s solution is more elegant, analogous to the Python solution in the next post. But as Gene pointed out, the more direct approach may be more efficient; it is for me, especially since I often do a lot of pre-computing in the constructor. I could see using the
bindapproach for some things. I’ve intended for some time to look into Boost, and this gives me one more reason.I thought maybe Boost was unnecessary, but the standard C++ library only has
bind1standbind2nd, so I guess you do need Boost for a more generalbindfunction.There’s no doubt that bind is a lot easier to use than bind1st and bind2nd. I just haven’t found it to be all that useful, compared to the technique you described in your paper. The implementation of bind used in boost is incredibly smart, I’m envious of the brainiac that came up with it.
To be honest, I really prefer to have the the function class implement an interface or abstract class rather than either of these solutions, but that’s another subject entirely.
Gene,
That smells like premature optimization to me. I would be very careful to measure in a /real/ program first. If you have such a program, I’d be interested.
Also, boost bind is not just for the nutters anymore: TR1 includes boost bind and boost function (of course, in the std namespace…)
Good post John.
Sorry for the double post but I’d like to expand.
Specifically, the original solution is not entirely unlike:
double
compute(double * a, double * b, double * c, double x)
{
return 1000* (*a) + 100 * (*b) + 10* (*c) + x;
}
Whereas the bind solution works out to approximately:
double
compute(double a, double b, double c, double d)
{
return 1000 * a + 100 * b + 10*c + d;
}
If we want to talk premature optimization, the first example can cause cache misses and all sorts of headache.
I’m interested in that real program of yours!
Gene,
When we wrote our numerical library, we had a debate between using abstract base classes and templates. My first thought was to use the former, but we ended up going with the latter. I don’t know whether we made the right choice.
Templates provide a form of “duck typing” in that you don’t have to derive your function objects from a particular base class. But using templates has lead to some ugly declarations when there are multiple function objects or nested function objects involved. It has also led to putting more code in .h files and less in .cpp files, which has its own set of pros and cons. I don’t know what I’d do if we started over.
John, I think if you are willing to take the overhead of a virtual function, then it is a no-brainer to have an abstract function object which has a child convenience class taking in a boost function. I can bet you 99% of the code will use the child convenience class though ;-)
Something like:
struct FunctObjBase
{
virtual ~FunctObjBase(){}
virtual double execute(double d) const = 0;
};
struct Helper : FunctObjBase
{
template
Helper(F const & f):
m_f(f){}
virtual double execute(double x){return m_f(0);}
private:
boost::function m_f;
};
Atleast thats what I’d do without evidence/requirements/proof to tell me otherwise.