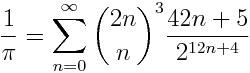Here are six people I have interviewed.
Vincent Tan interviewed me here.
This morning I had a fun support request related to our software. The exchange took place over email but it could have fit into a couple Twitter messages. Would that all requests could be answered so succinctly.
Question:
Do you have R code to compute P(X > Y) where X ~ gamma(ax, bx) and Y ~ gamma(ay, by)?
Response:
ineq <- function(ax, bx, ay, by) pbeta(bx/(bx+by), ay, ax)
For more on the problem and the solution, see Exact calculation of inequality probabilities.
Related links:
From Nigel Marsh:
I stepped back from the workforce and I spent a year at home with my wife and four young children. But all I learned about work-life balance from that year was that I found it quite easy to balance work and life when I didn’t have any work.
The following algorithm is based on work of Ramanujan and has been used in several world-record calculations of pi.
Initialize a0 = 6 – 4 √2 and y0 = √2 – 1. Then compute
and
The terms an form a sequence of approximations to 1/π. The error in each approximation is given by
This says that the number of correct digits roughly quadruples after each step. To see this, note that the number of correct decimal places after the nth step is the negative of the logarithm base 10 of the error:
[The error term goes to zero so quickly that you cannot (in ordinary precision) compute the error bound and then take logarithms; the exp(-2 π 4n) term will underflow to zero for n larger than 3. (See why here.) You have to take the log of the error term directly before evaluating numerically.]
The number of correct digits quadruples at each step because the leading term in the numerator above is 4n.
To give a few specifics, a1 is accurate to 9 digits, a2 is accurate to 41 digits, and a3 is accurate to 171 digits. After 10 steps, a10 is accurate to over 2.8 million digits.
The algorithm given here was state of the art as of 1989. It was used to set world records in 1986. I don’t know whether it has been used more recently. See more here.
According to this page, π has been calculated to 6.4 billion digits. You can beat this record if you can carry out 16 steps of the method described here. a16 would be accurate to over 11 billion digits.
Update (18 April 2012): The algorithm used most recently for world record calculations for pi has been the Chudnovsky algorithm. As of October 2011, the record was over 10 trillion digits.
Ramanujan discovered the following remarkable formula for computing π:
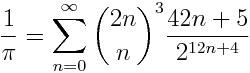
This is not the most efficient series for computing π. My next post will give a more efficient method, also based on work of Ramanujan. But the series above is interesting for reasons explained below.
Notice that the denominator of each term in the sum above is a power of 2. This means the partial sums of the series can be represented exactly in binary. We’ll see that each term in the series adds six bits precision to the sum once we’ve added enough terms.
To understand how to use this series, we need to estimate the binomial coefficient term. Stirling’s approximation shows that
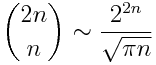
This tells us that the nth term in the series is a rational number with numerator something like 2^6n and denominator 2^(12n+4). Therefore the nth term is on the order of 2^(-6n-4) and so the series converges quickly. The first three terms illustrates this:
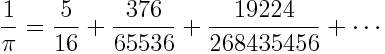
The error in summing up a finite number of terms is approximately the first term in the remainder, so just a few terms leads to an accurate approximation for 1/π and hence an accurate approximation for π.
To be a little more precise, when we sum the series from n = 0 to n = N, the error in approximating 1/π is on the order of the next term, 2^(-6N-10). Said another way, summing up to the Nth term computes 1/π to 6N + 10 bits. For example, suppose we wanted to compute 1/π to 200 decimal places. That’s about 664 bits, and so 108 terms of the series should be enough.
We glossed over a detail above. We said that the nth term is on the order of 2^(-6n-4). That’s true for sufficiently large n. In fact, we can say that the nth term is less than 2^(-6n-4), but only for large enough n. How large? We need the denominator term (π n)^3/2 to be larger than the numerator term 42n + 5. This happens if n is at least as large as 58.
One advantage to using this series to compute π is that you could compute later blocks of bits without having to compute the earlier blocks, provided you’re interested in the bits beyond those contributed by 58th term in the series.
Related post: Two useful asymptotic series
William Turkel has a nice four-part series of blog posts entitled A Workflow for Digital Research Using Off-the-Shelf Tools. His four points are
Also by William Turkel, The Programming Historian, “an open-access introduction to programming in Python, aimed at working historians (and other humanists) with little previous experience.”
Related post: Create offline, analyze online
From Dave Ewing via Roberto Montagna:
The headline you won’t be reading: “Millions saved in Japan by good engineering and government building codes”. But it’s the truth.
The loss of life in Japan is tragic, but it would have been far worse without good engineering.
Update: As Tim points out in the comments below,The New York Times did publish a story headlined Japan’s Strict Building Codes Saved Lives. This is to be commended since it’s natural to only see the people who died and not the people who did not. Along these lines, I wonder how many people did not die mining coal to generate the electricity that nuclear power has provided Japan.
From Douglas Copeland’s book on Marshall McLuhan:
Marshall … didn’t have the patience to work through a book that didn’t interest him from the start. He even developed a technique to suit his impatience: whenever he picked up a new book, he would turn to page 69, and if that page didn’t interest him, he wouldn’t read the book.
Marshall McLuhan: You Know Nothing of My Work!
Related post: Reading as inclination leads
The previous post showed how to list all limerick primes. This post shows how to list all sonnet primes. These are primes of the form ababcdcdefefgg, the rhyme scheme of an English (Shakespearean) sonnet, where the letters a through g represent digits and a is not zero.
Here’s the Mathematica code.
number[s_] := 10100000000000 s[[1]] + 1010000000000 s[[2]] +
1010000000 s[[3]] + 101000000 s[[4]] +
101000 s[[5]] + 10100 s[[6]] + 11 s[[7]]
test[n_] := n > 10^13 && PrimeQ[n]
candidates = Permutations[Table[i, {i, 0, 9}], {7}];
list = Select[Map[number, candidates], test];
The function Permutations[list, {n}] creates a list of all permutations of list of length n. In this case we create all permutations the digits 0 through 9 that have length 7. These are the digits a through g.
The function number turns the permutation into a number. This function is applied to each candidate. We then select all 14-digit prime numbers from the list of candidates using test.
If we ask for Length[list] we see there are 16,942 sonnet primes.
As mentioned before, the smallest of these primes is 10102323454577.
The largest is 98987676505033.
Related post: Limerick primes
The other day, Futility Closet posted this observation:
10102323454577 is the smallest 14-digit prime number that follows the rhyme scheme of a Shakespearean sonnet (ababcdcdefefgg).
I posted this on AlgebraFact and got a lot of responses. One was from Matt Parker who replied that 11551 was the smallest prime with a limerick rhyme scheme.
So how many limerick primes are there? Well, there aren’t many candidates. A limerick prime has to have the form AABBA where A is an odd digit and B is any digit other than A. So for each of five choices of A, there are nine possible B’s. Here’s a Mathematica program to do a brute force search for limerick primes.
For[ j = 0, j < 5, j++,
For[ k = 0, k < 10, k++,
x = (2 j + 1)*11001 + 110 k;
If[ PrimeQ[x], Print[x] ]]]
It turns out there are eight limerick primes:
See the next post for Mathematica code to list all sonnet primes.
Update: See Lawrence Kesteloot’s code for a different kind of Limerick prime, a number that sounds like limerick when read outloud.