Golden strings are analogous to Fibonacci numbers, except one uses concatenation rather than addition.
Start with s1 = “1” and s2 = “10”. Then define sn = sn-1 + sn-2 where “+” means string concatenation.
The first few golden strings are
- “1”
- “10”
- “101”
- “10110”
- “10110101”
- …
The length of sn is Fn+1, the n+1st Fibonacci number. Also, sn contains Fn 1’s and Fn-1 0’s. (Source: The Glorious Golden Ratio).
If we interpret the sn as the fractional part of a binary number, the sequence converges to the rabbit constant R = 0.7098034428612913…
It turns out that R is related to the golden ratio φ by
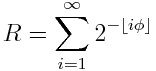
where ⌊i φ⌋ is the largest integer no greater than iφ.
Here’s a little Python code to print out the first few golden strings and an approximation to the rabbit constant.
from mpmath import mp, fraction
a = "1"
b = "10"
for i in range(10):
b, a = b+a, b
print(b)
n = len(b)
mp.dps = n
denom = 2**n
num = int(b, 2)
rabbit = fraction(num, denom)
print(rabbit)
Note that the code sets the number of decimal places, mp.dps, to the length of the string b. That’s because it takes up to n decimal places to exactly represent a rational number with denominator 2n.

The rabbit constant calculation in the J language:
0.5#.|.0,;(;;{.)^:(6) 1;0
0.709803
written by Raul Miller @ forums.jsoftware.com
In Haskell:
gold = “1”:”10″:zipWith (++) (tail gold) gold
The latest version of sympy no longer ships with mpmath. You should change the code to just use “from mpmath import …”.
Thanks, Aaron. I updated the post as you suggested.