Sum of geometric means

Posted on by John

Let xn be a sequence of non-negative numbers. Then the sum of their running geometric means is bounded by e times their sum. In symbols

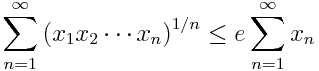
\sum_{n=1}^\infty \left(x_1 x_2 \cdots x_n\right)^{1/n} \leq e \sum_{n=1}^\infty x_n

The inequality is strict unless all the x‘s are zero, and the constant e on the right side is optimal. Torsten Carleman proved this theorem in 1923.

5 thoughts on “Sum of geometric means”

  2. John

    If the sum diverges, the right side is ∞ and so the inequality holds.

    However, the statement after the equation does require convergence: “The inequality is strict unless all the x‘s are zero, and the constant e on the right side is optimal.” If all x are 1, for example, both sides diverge and so in a sense you have equality, not a strict inequality.

  3. Mike G.

    Interesting. It’s one of those things in math that are odd to me on several levels:

    1) Why would that be the case? The relationship between the 2 values isn’t obvious at all.

    2) Ok, I’ll admit, the guy proved it, so it is the case. WHY did he even think of proving it? :)

    3) Finally, even though I’m sure I wouldn’t understand the answer, I’m curious as to HOW he proved it.

    It’s not often one of these mathematical curiosities has all these levels of puzzlement for me :)

  5. Wolfgang Tintemann

    The result looks almost divine at first look.

    But has it any use somewhere ? Was it used to prove any other result ?
    Where did you meet it in the world of math or is it a lonely formula ?

Comments are closed.