A beta(a, b) distribution is approximately normal if the parameters a and b are large and approximately equal. A beta(a,b) distribution has mean a/(a+b) and variance ab/(a+b)2(a+b+1). When a=b, this reduces to mean 1/2 and variance 1/(8a + 4).
The following graph shows the difference between the CDF of a beta(5,5) distribution and the CDF of normal distribution with the same mean and variance, i.e. mean 1/2 and variance 1/44.
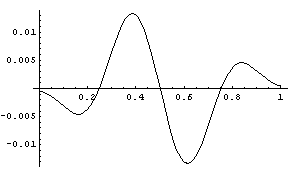
As the beta parameters increase, the amplitude of the error curve decreases and the curve shrinks toward the middle. Below is a graph of the CDF of a beta(20,20) distribution minus the CDF of a normal with mean 1/2 and variance 1/164.
The error curve for ν = 30 is below.
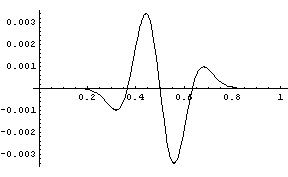
Here is the maximum error as a function of the common beta parameter.
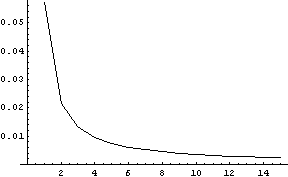
The quality of the approximation degrades when the a and b parameters are not approximately equal. Also, when the parameters are not equal, the error function loses its symmetry. For example, for a beta(40,40) distribution, the error curve resembles the error curves above and has a maximum value of 0.0017. The error curve for the normal approximation to a beta(30,50) distribution is given below.
The maximum error is about 0.008, over twice the error in the normal approximation to a beta(30,30) distribution and over four times the error in the normal approximation to a beta(40,40) distribution.
In 1960, Wise published a transformation that improves the normal approximation to the beta (Biometrika vol 47, No. 1/2, June 1960, pp. 173-175). If X is a beta(a, b) random variable with a ≥ b, (-log X)1/3 is more nearly normal than X is.
Here we show how well Wise’s transformation works for X ~ beta(5,4). The follow graph shows the PDFs of X and its normal approximation.
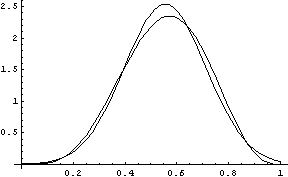
The graph below shows the difference in the CDFs of the two distributions.
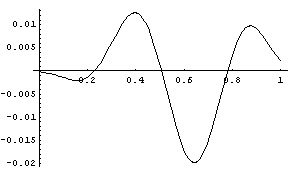
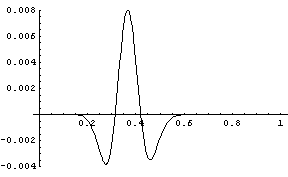
Next we apply Wise’s transformation. The random variable Y = (-log X)1/3 has mean 0.835 and variance 0.0209. When we plot the PDFs of the two distributions, graphs appear to lie on top of each other. The following is the graph of the difference between the CDF functions.
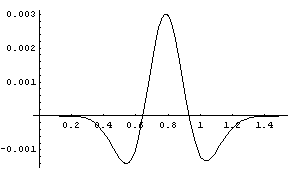
The maximum error has been reduced from about 0.02 to about 0.003.
Note that this page has only considered absolute error in the normal approximation. The relative error is a different story.
See also notes on the normal approximation to the binomial, gamma, Poisson, and student-t distributions.
