In my previous post, I discussed how number theory and topology relate to other areas of math. Part of that was to show a couple diagrams from Jean Dieudonné’s book Panorama of Pure Mathematics, as seen by N. Bourbaki. That book has only small star-shaped diagrams considering one area of math at a time. I’ve created a diagram that pastes these local views into one grand diagram. Along the way I’ve done a little editing because the original diagrams were not entirely consistent.
Here’s a condensed view of the graph. You can find the full image here.
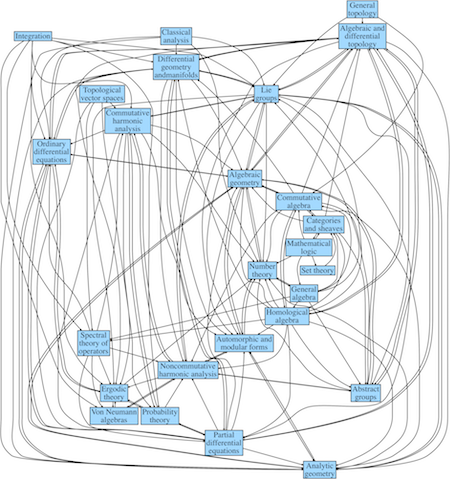
The graph is so dense that it’s hard to tell which areas have the most or least connections. Here are some tables to clarify that. First, counting how many areas an particular area contributes to, i.e. number of outgoing arrows.
|-------------------------------------+---------------| | Area | Contributions | |-------------------------------------+---------------| | Homological algebra | 12 | | Lie groups | 11 | | Algebraic and differential topology | 10 | | Categories and sheaves | 9 | | Commutative algebra | 9 | | Commutative harmonic analysis | 9 | | Algebraic geometry | 8 | | Differential geometry and manifolds | 8 | | Integration | 8 | | Partial differential equations | 8 | | General algebra | 7 | | Noncommutative harmonic analysis | 6 | | Ordinary differential equations | 6 | | Spectral theory of operators | 6 | | Analytic geometry | 5 | | Automorphic and modular forms | 5 | | Classical analysis | 5 | | Mathematical logic | 5 | | Abstract groups | 4 | | Ergodic theory | 4 | | Probability theory | 4 | | Topological vector spaces | 4 | | General topology | 3 | | Number theory | 3 | | Von Neumann algebras | 2 | | Set theory | 1 | |-------------------------------------+---------------|
Next, counting the sources each area draws on, i.e. counting incoming arrows.
|-------------------------------------+---------| | Area | Sources | |-------------------------------------+---------| | Algebraic geometry | 13 | | Number theory | 12 | | Lie groups | 11 | | Noncommutative harmonic analysis | 11 | | Algebraic and differential topology | 10 | | Analytic geometry | 10 | | Automorphic and modular forms | 10 | | Ordinary differential equations | 10 | | Ergodic theory | 9 | | Partial differential equations | 9 | | Abstract groups | 8 | | Differential geometry and manifolds | 8 | | Commutative algebra | 6 | | Commutative harmonic analysis | 6 | | Probability theory | 5 | | Categories and sheaves | 4 | | Homological algebra | 4 | | Spectral theory of operators | 4 | | Von Neumann algebras | 4 | | General algebra | 2 | | Mathematical logic | 1 | | Set theory | 1 | | Classical analysis | 0 | | General topology | 0 | | Integration | 0 | | Topological vector spaces | 0 | |-------------------------------------+---------|
Finally, connectedness, counting incoming and outgoing arrows.
|-------------------------------------+-------------| | Area | Connections | |-------------------------------------+-------------| | Lie groups | 22 | | Algebraic geometry | 21 | | Algebraic and differential topology | 20 | | Noncommutative harmonic analysis | 17 | | Partial differential equations | 17 | | Differential geometry and manifolds | 16 | | Homological algebra | 16 | | Ordinary differential equations | 16 | | Analytic geometry | 15 | | Automorphic and modular forms | 15 | | Commutative algebra | 15 | | Commutative harmonic analysis | 15 | | Number theory | 15 | | Categories and sheaves | 13 | | Ergodic theory | 13 | | Abstract groups | 12 | | General algebra | 10 | | Spectral theory of operators | 10 | | Probability theory | 9 | | Integration | 8 | | Mathematical logic | 6 | | Von Neumann algebras | 6 | | Classical analysis | 5 | | Topological vector spaces | 4 | | General topology | 3 | | Set theory | 2 | |-------------------------------------+-------------|
There are some real quirks here. The most foundational areas get short shrift. Set theory contributes to only one area of math?! Topological vector spaces don’t depend on anything, not even topology?!
I suspect Dieudonné had in mind fairly high-level contributions. Topological vector spaces, for example, obviously depend on topology, but not deeply. You could do research in the area while seldom drawing on more than an introductory topology course. Elementary logic and set theory are used everywhere, but most mathematicians have no need for advanced logic or set theory.

So which nodes have the highest degrees? Are there some areas only linked by a one way arrow?
I’ve updated the post to address your question quantitatively. I’m removing my previous answer because I’ve incorporated much of it into the post.
When I was getting my PhD, I recall the conventional wisdom around my department being that if you only had the standard undergrad background (that is, a strong undergraduate math major from one of our peer institutions) coming into the program, there’s no way you could get a PhD in algebraic geometry. This seems consistent with algebraic geometry having a high indegree. If memory serves, many of the people who did eventually write theses on algebraic geometry either came in with a Master’s degree or did their undergraduate work outside of the US, where undergraduate work tends to be more focused.
Michael: That sounds right. John Tate came to UT while I was there, and seems like his students took forever to graduate.
I had some interest in differential geometry, but it seemed like you needed to study for years before you ever got down to geometry. The people in that area took a long time to graduate too.
PDE is well connected — that’s one reason I went into that area — but the prerequisites aren’t that bad, maybe more broad than deep. Or maybe I just had a background that lined up well with what PDEs required. The folks in our group graduated without hanging around too long.
After going into industry, I’ve had more use for the things I learned in the context of PDEs than I’ve had for PDEs per se.
Could I find an adjacency matrix for this somewhere?
Hi John, I suggest redoing it, giving different nodes different colors, and coloring edges by the color of one of the two nodes it connects to (although which one has to be arbitrary since it’s undirected). Maybe the color of the denser node? Just a thought.
Oh, I see, it *is* directed, so that gives you a principled way to do it. Sorry, hadn’t read the whole post yet.
As you say, “Dieudonné had in mind fairly high-level contributions.” Doing this with individual results/theorems instead of whole branches would be elucidating. Maybe when math becomes more digitized.