A catenary with scale a is the graph of the function
f(x; a) = a cosh(x/a) – a.
The x and the a are separated by a semicolon rather than a comma to imply that we think of x as the variable and a as a parameter.
This graph passes through the origin, i.e. for any a, f(0, a) = 0. To find the scaling parameter a we need to specify the value of f at one more point and solve f(x, a) = y. This is the equation I alluded to recently as not having a closed-form solution.
Without loss of generality, we can assume x = 1. Why is that?
Define
g(a) = f(1; a).
Then
f(x‘; a‘) = y‘
if and only if
g(a‘/x‘) = y‘/x‘.
So will assume x = 1 for now and focus on solving for a value of a such that g(a) = y. But we will include Python code shortly that goes back to f, i.e. does not assume x = 1.
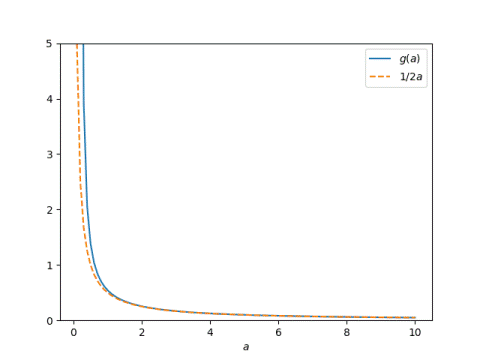
The Taylor series for g looks like
g(a) = 1 / 2a + 1 / 24a³ + …
and so for large a,
g(a) ≈ 1 / 2a.
Here are a couple plots showing how good this approximation is, even for a not that large. First, a plot of g and its approximation.
And here’s a plot of the relative error in approximating g(a) by 1/2a.
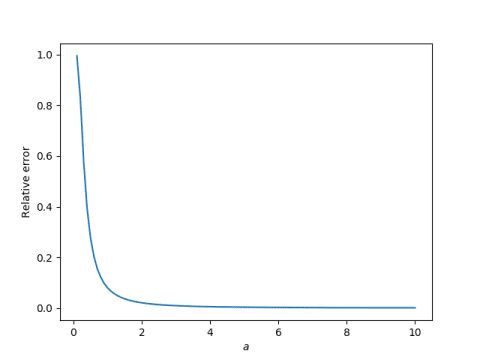
This means that for small y,
g(1 / 2y) ≈ y.
It’s fortunate that we have a convenient approximation when y is small, because in practice y is usually small: catenaries are usually wider than deep, or at least not much deeper than wide.
Since the terms in the Taylor series that we discarded are all positive, we also have a bound
g(1 / 2y) > y.
If we want to solve for a numerically, 1 / 2y makes a good starting guess, and it also makes a left bracket for root-finding methods that require a bracket around the root.
Here’s Python code to solve f(x, a) = y for a, given x and y.
from numpy import cosh
from scipy.optimize import root
def g(a):
return a*cosh(1/a) - a
def solve_g(y):
assert(y > 0)
lower = 0.5/y
return root(lambda a: g(a) - y, lower).x
def solve_catenary(x, y):
"Solve for a such that a cosh(x/a) - a == y."
return x*solve_g(y/abs(x))
Now that we can solve g(a) = y numerically, we can go back and see how far 1 / 2y is from the actual solution for varying values of y.
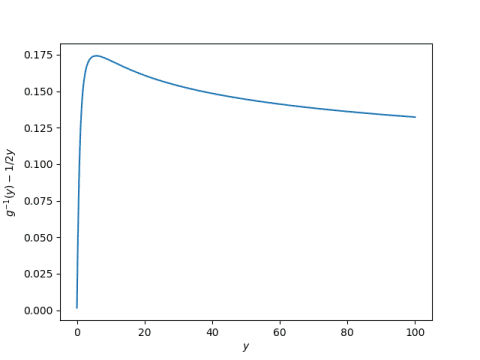
Recall that the second plot above showed that the relative error in approximating g(a) by 1 / 2a is large when a is small (and thus y is big). But the plot immediately above shows that nevertheless, 1/ 2y is a good guess at a solution to g(a) = y, never off by more than 0.175.
Recall also that we said 1 / 2y is a lower bound on the solution, and could be used as a left bracket in a root-finding method that requires a bracket. The plot above suggests that 0.18 + 1 / 2y would work as a right bracket

For “eluded” read “alluded”.