Convert loudness between phon and sone units

Loudness

Loudness is the perceived intensity of sound. Sound pressure level is the physical intensity of a sound. The relation between the two is complicated. Follow this link for an introduction to quantifying loudness.

Phon

For a pure tone at 1 kHz, loudness in phon equals sound pressure level in decibels (dB). For pure tones at much higher or lower frequency, loudness in phon will be less than sound pressure level in dB because hearing is less sensitive as you move away from the neighborhood of 1 kHz. The loudness of complex sounds, i.e. not pure tones, is complex. In addition to hearing sensitivity varying with frequency, in complex sounds some sound components partially mask other components.

Sone

The unit of phon is based on sound pressure measured on a logarithmic (dB) scale. Sone is a more linear scale of perception. Increasing loudness by 10 phon increases loudness in sone by a factor of 2. (This is true for sounds louder than 40 phon. Things change for very soft sounds for reasons explained below.)

Conversion between units

Loudness of 40 phon equals loudness of 1 sone. For loudness above 40 phon or 1 sone,

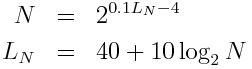
$N &=& 2^{0.1L_N - 4} \\ L_N &=& 40 + 10 \log_2 N$

and for loudness below 40 phon or 1 sone,

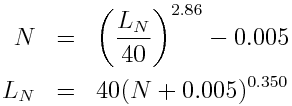
$N &=& \left(\frac{L_N}{40}\right)^{2.86} - 0.005 \\ L_N &=& 40 (N + 0.005)^{0.350}$

Why the change at 40 phon? Because human perception changes at about 40 dB. For a 1 kHz tone above 40 dB, perceived loudness doubles every 10 dB. But below 40 dB, perceived loudness drops off more quickly; it takes less than a 10 dB reduction in sound pressure level below 40 dB in order for humans to perceive the loudness as having been cut in half. The phon scale sticks to the dB level of a 1 kHz tone, even for sounds quieter than 40 dB. The sone scale attempts to follow human perception for all sound pressure levels so that, for example, doubling the loudness of a sound doubles its value in sone.

Reference: Psychoacoustics: Facts and Models by Hugo Fastl and Eberhard Zwicker

More calculators like this one.

Is there anything else I can help you with? Maybe something with acoustics?