Relationships between Bessel functions

The relationships between the various kinds of Bessel functions are summarized in the diagram below.

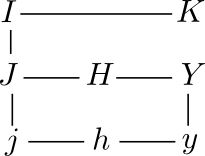
The functions in the left column are functions “of the first kind” and the functions in the right column are functions “of the second kind.” The functions in the middle column are “Hankel functions.” The functions in each row satisfy a particular differential equations. The lines between functions represent simple relationships. Details are given below.

Basic Bessel functions

The most basic Bessel functions are the functions J_ν(z) imaginatively named “Bessel functions of the first kind.” I won’t go into their definition here, but I’ll explain how all the other functions in the Bessel function family reduce to these functions. For definitions and numerous identities, see functions.wolfram.com.

The functions Y_ν(z) are called the “Bessel functions of the second kind.” They are linear combinations of J_ν and J_-ν:

$Y_\nu(z) = \cot(\pi\nu) J_\nu(z) - \csc(\pi\nu) J_{-\nu}(z)$

Why define the functions Y_ν? They Y_ν functions are independent solutions to the differential equation that motivated the functions J_ν. Specifically, J_ν and Y_ν form a basis for the solutions to Bessel’s equation

In general, functions “of the second kind” were created to form independent solutions to a differential equation satisfied by the corresponding function of the first kind.

Hankel functions

The Hankel functions are linear combinations of the Bessel functions of the first and second kind.

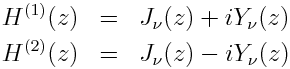
$H^{(1)}(z) = J_\nu(z) + i Y_\nu(z); H^{(2)}(z) = J_\nu(z) - i Y_\nu(z)$

Spherical Bessel functions

Next we come to the spherical Bessel functions, so named because they arise when solving the Helmholtz equation in spherical coordinates.

For integers n, the functions j_n and y_n are related to the functions J_{n + ½} and Y_{n + ½}.

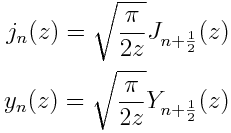
$j_n(z) = \sqrt{\frac{\pi}{2z}} J_{n+\frac{1}{2}}(z) \\ y_n(z) = \sqrt{\frac{\pi}{2z}} Y_{n+\frac{1}{2}}(z)$

Spherical Hankel functions

The spherical Bessel functions have their Hankel function counterparts h⁽¹⁾_n and h⁽²⁾_n. These are formed from j_n and y_n exactly the same way H⁽¹⁾_n and H⁽²⁾_n are formed from J_n and Y_n.

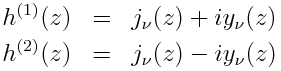
$h^{(1)}(z) = j_\nu(z) + i y_\nu(z); h^{(2)}(z) = j_\nu(z) - i y_\nu(z)$

Modified Bessel functions

Finally we have the functions I_ν and K_ν, the “modified Bessel functions of the first and second kind.” I_ν is essentially J_ν with its argument rotated. Specifically

$I_\nu(z) = i^{-\nu} J(iz)$

Also, the functions K_ν are related to the functions I_ν analogously to the way the Y_ν are related to the J_ν, namely

$K_\nu(z) = \frac{\pi}{2\sin\pi\nu} \left(I_{-\nu}(z) - I_\nu(z) \right)$

The functions I_ν and K_ν are independent solutions to the modified Bessel differential equation

The modified Bessel functions of the second kind were also known by several names that are seldom used anymore.

Basset functions
Modified Bessel functions of the 3rd kind
Modified Hankel functions
Macdonald’s functions

The diagram would be symmetric if K_ν were as simply related to Y_ν as I_ν is related to J_ν. Unfortunately, that is not the case.

Other diagrams on this site

See this page for more diagrams on this site including diagrams for probability and statistics, analysis, topology, and category theory.