Real analysis studies four basic modes of convergence for a sequence of functions fn on a measure space Ω with measure μ.
- Almost everywhere (AE). The sequence fn converges almost everywhere to f if fn(x)converges to f(x) except possibly for a set of x values of measure zero.
- Almost uniform (AU). The sequence fn converges almost uniformly if for every ε > 0 there exists a corresponding set Aε of measure less than ε such that fn converges uniformly to f on the complement of Aε.
- Lp. The sequence fn converges to f in Lp norm if
- In measure (M). The sequence fn converges to f in measure if for every ε> 0,
In probability and statistics, convergence in measure is called convergence in probability.
This page summarizes and diagrams the relations between these four modes of convergence in general, in a finite measure space, and under dominated convergence. Then counterexamples are given that show no more relationships exist in general.
Diagrams
The relationships between the various modes of convergence can be summarized in the diagram below. A solid line means that convergence in the mode at the tail of the arrow implies convergence in the mode at the head. A dashed line means that convergence in the mode at the tail of the arrow implies the existence of a subsequence that converges in the mode at the head of the arrow. (The idea for this kind of diagram came from Elements of Integration by Robert Bartle, 1966.)
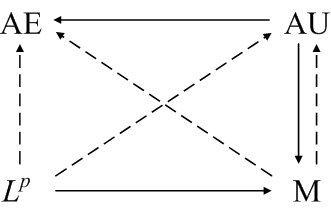
General measure spaces
The first diagram shows the general relationships between the four modes of convergence.
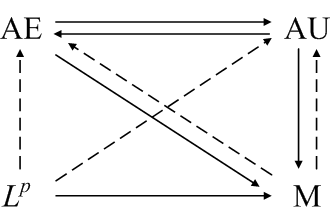
Finite measure spaces
Now suppose μ(Ω). For finite measure spaces, almost everywhere and almost uniform convergence are equivalent. Convergence in measure is the weakest form of convergence since it is implied by the other forms. The following diagram summarizes the relationships between the four modes of convergence for finite measure spaces.
Dominated convergence
If Ω is a general measure space, but the sequence fn is uniformly dominated by an Lp function g, then more relationships exist, as summarized in the diagram below.
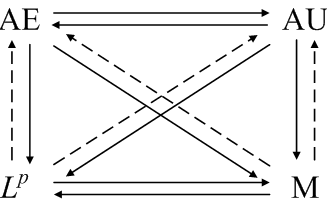
Note that the even though we do not require Ω to be a finite measure space, all the convergence relationships for finite measure spaces continue to hold, as well as two new ones.
In this setting, almost everywhere and almost uniform convergence are equivalent. Also, Lp convergence and convergence in measure are equivalent.
Counterexamples
Three counter examples suffice to prove that the diagrams above are complete. When an interval is referred to as a function, the function is the indicator function of that interval.
First, consider the functions [0, 1], [0, 1/2], [1/2, 1], [0, 1/3], [1/3, 2/3], etc. The sequence fn converges to 0 in measure and in Lp. However, there is no x for which fn(x) converges to 0 (fn(x) = 1 infinitely often) and so fn converges neither almost everywhere nor almost uniformly. Note that in this case Ω = [0, 1] is a finite measure space, and the constant function 1 is an Lp bound on the sequence.
Next, consider the functions fn = n [1/n, 2/n]. The sequence fn converges pointwise to 0 everywhere. It converges almost uniformly and converges in measure. However, the Lp norm of fn is 1 for all n and so no subsequence converges to 0 in Lp norm. Note again Ω = [0, 1] is a finite measure space in this example.
Finally, let fn be [n, n+1]. Then fn converges to 0 everywhere, but fn does not converge in measure. In this case Ω is not a finite measure space.
Probability
In probability theory, almost everywhere convergence is called almost certain convergence or almost sure convergence. Convergence in measure is called convergence in probability. The measure space in question is always finite because probability measures assign probability 1 to the entire space.
In a finite measure space, almost everywhere convergence implies convergence in measure. Therefore almost convergence implies convergence in probability.
Convergence in measure is the weakest form of convergence generally studied in analysis, but in probability theory there is an even weaker form of convergence, convergence in distribution. A sequence of random variables converges in distribution if their corresponding distribution functions converge pointwise. Convergence in probability implies convergence in distribution.
The weak law of large numbers is an example of convergence in probability. The strong law of large numbers is an example of almost certain convergence. The central limit theorem is an example of convergence in distribution.
Other mathematical diagrams
See this page for more diagrams on this site including diagrams for probability and statistics, analysis, topology, and category theory.
