Two ways of generalizing π

The constant π is the ratio of a circle’s circumference to its diameter. We can generalize π by generalizing what a circle is. We will define a p-circle to be the solution to

for 1 ≤ p ≤ ∞. The case of p = ∞ is defined as the limit of the cases of p as p → ∞.

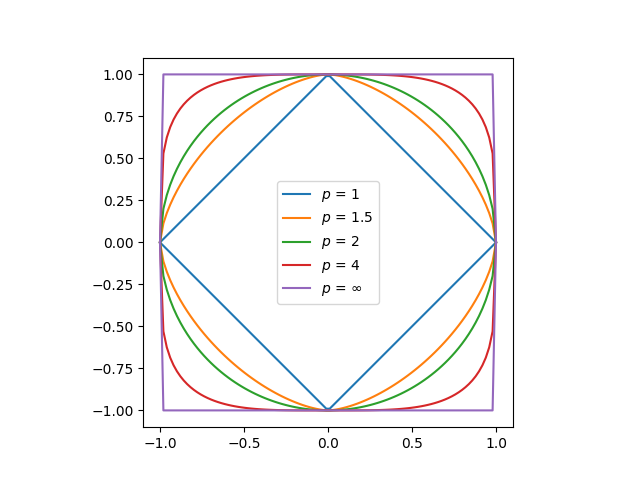
Here’s what p-circles look like for p = 1, 1.5, 2, 4, and ∞.

First approach

We could define π_p as the ratio of the perimeter of a p-circle to its diameter. When p = 2 we get π, so π₂ is just π. And we can see that π₁ = 2√2 and π_∞ = 4.

We might ask for what value of p does π_p = 3. Evidently for some value between 1 and 2, which we can find numerically to be 1.5815 using the Python code from this post.

Confession: I stretched the truth a little in the plot above. The curve labeled p = 1.5 actually corresponds to p = 1.5815, so the circumference of the orange curve above is exactly 6. (The difference between a 1.5-circle and a 1.5815-circle is hardly noticeable.)

The approach above is one way to generalize π, and it is the approach taken in “squigonometry.”

Second approach

There’s an inconsistency in the approach above. We’ve changed our definition of circle without changing our definition of arc length. We could say a p-circle is the set of points with constant distance to the center, as measured in the p-norm metric.

This is consistent with the definition above. However, when we also measure the circumference of the p-circle in the p-norm metric we get a different circumference and hence a different definition of π_p.

As before, π₂ = π and π_∞ = 4. But with this new definition π₁ = 4. How is this? The 1-circle is a diamond, and the length of one side of this diamond is √2 in the Euclidean (2-norm) metric, but the length is 2 in the 1-norm metric.

Comparison plots

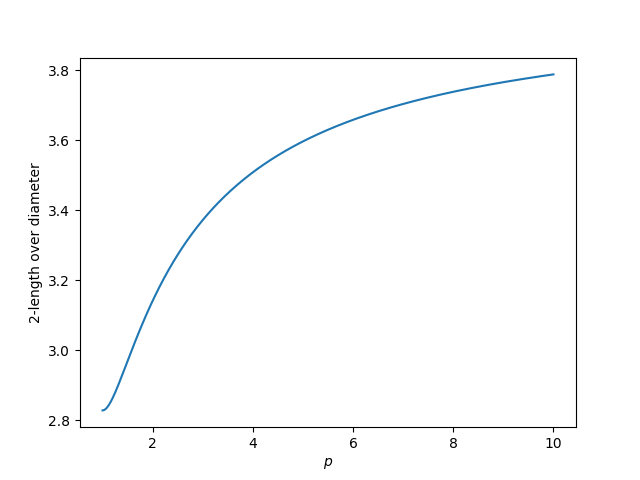
Under the first definition of π_p, computing the perimeter of a p-circle using the 2-norm, π_p is an increasing function of p.

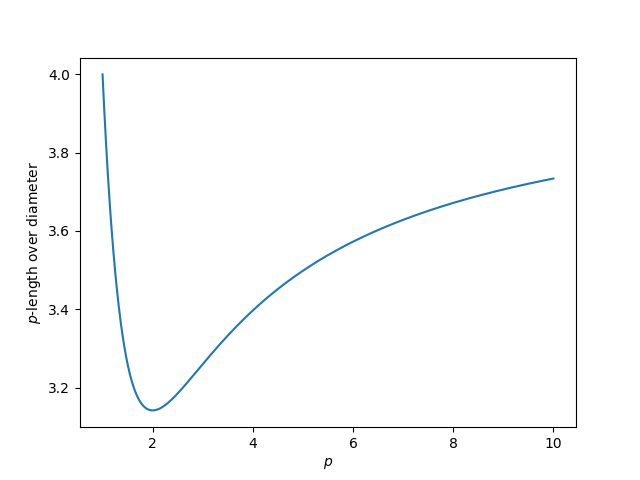
Under the second definition π_p, computing the perimeter of a p-circle using the p-norm, π_p is not a monotone function of p. Instead, π_p starts at 4 when p = 1, decreases to a minimum at p = 2, and increases asymptotically to 4 as p → ∞. Or as the title of [1] puts it, “π is the minimum value for pi.”

[1] C. L. Adler, James Tanton. π is the Minimum Value for Pi. The College Mathematics Journal, Vol. 31, No. 2 (Mar., 2000), pp. 102-106