Error in normal approximation Poisson

This page is an appendix to the page Error in the normal approximation to the Poisson distribution.

The previous page noted that a Poisson random variable with mean λ has the same distribution as the sum of N independent Poisson random variables X_i each with mean λ/N. The Berry-Esséen theorem says that the error in approximating the CDF of ∑X_i with the CDF of its normal approximation is uniformly bounded by C ρ/σ³√N where C is a constant we discuss below, ρ = E(|X_i − λ/N|³) and σ, the standard deviation of X_i, equals (λ/N)^1/2.

Since the number N is arbitrary, we pick it as large as we like. This paper says the constant in the Berry-Esséen theorem can be made less than 0.7164 if N ≥ 65. This is no problem here because we will be taking the limit as N goes to infinity.

Next we calculate ρ, the third absolute moment of X_i. Let ω = λ/N. We can get an upper bound on ρ as follows.

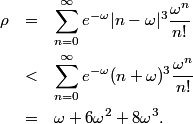
$\begin{eqnarray*}<br /> \rho \sum_{n=0}^\infty e^{-\omega} | n - \omega |^3 \frac{\omega^n}{n!} \\<br /> \sum_{n=0}^\infty e^{-\omega} (n + \omega)^3 \frac{\omega^n}{n!} \\<br /> \omega + 6\omega^2 + 8\omega^3.<br /> \end{eqnarray*}$

From this we can conclude that ρ/σ³√N equals λ plus term involving 1/N. As we let N to infinity, the latter terms drop out and so we have the error bound on the normal approximation to the Poisson of C/√λ where C < 0.7164.