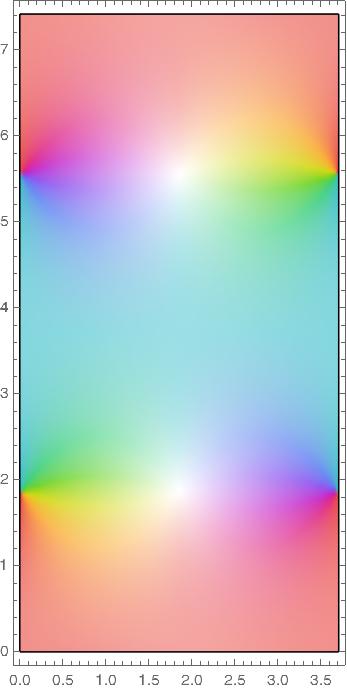
Elliptic functions are doubly periodic and so their values everywhere in the complex plane are determined by their values in a fundamental parallelogram. We will assume the parameter m is real and between 0 and 1 so that the fundamental parallelograms are rectangles aligned with the real and imaginary axes.
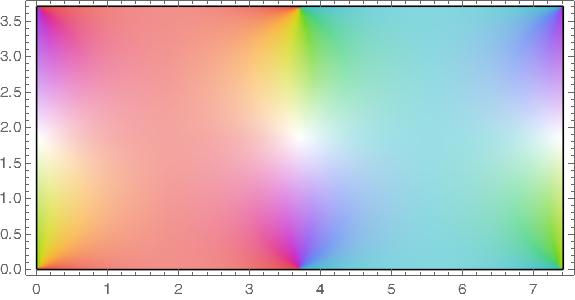
The functions sn, ns, cd, and dc all have a fundamental rectangle with vertices at o and 4K(m) + 2K(1 − m) i.
The functions cn, nc, ds, and sd all have a fundamental rectangle with vertices at o and 4K(m) + 4K(1 − m) i.
The functions cs, sc, dn, and nd all have a fundamental rectangle with vertices at o and 2K(m) + 4K(1 − m) i.
In the plots below m = 1/2 so that m = 1 − m.
Pinwheels of color indicate zeros and white areas indicate poles.
Note that the reciprocal of a function swaps the letters in the name, e.g. ns(z) = 1/sn(z). Taking the reciprocal swaps zeros and poles.
sn
This function was plotted in Mathematica using
K = EllipticK[1/2]
ComplexPlot[JacobiSN[z, 1/2],
{z, 0, 4 K + 2 I K},
AspectRatio -> Automatic]
and the rest of the plots were made analogously.
ns
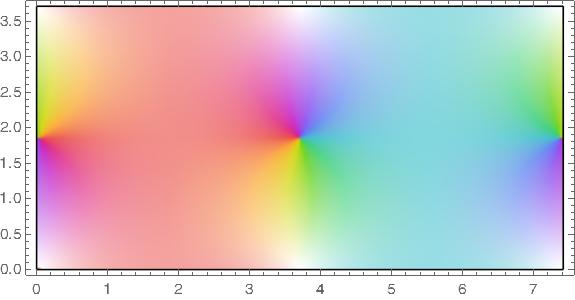
cd
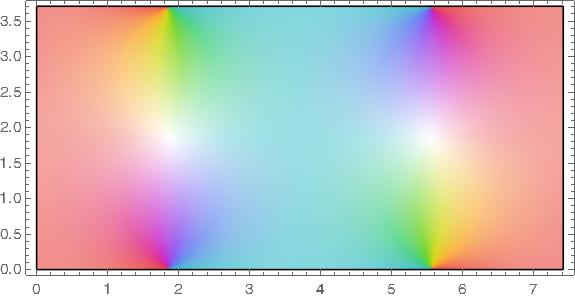
dc
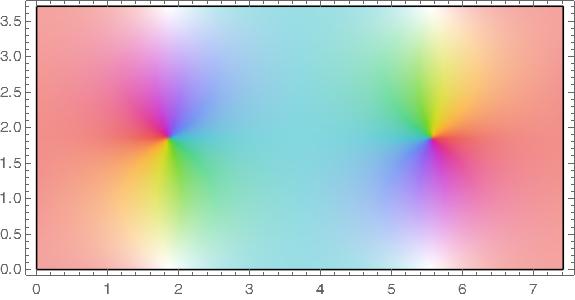
cn
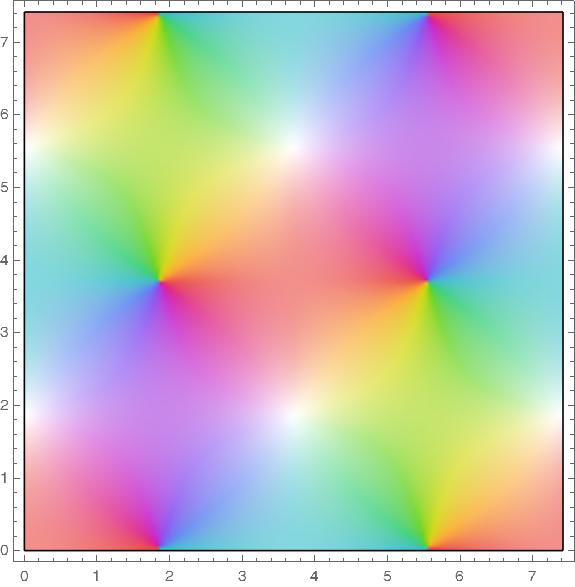
nc
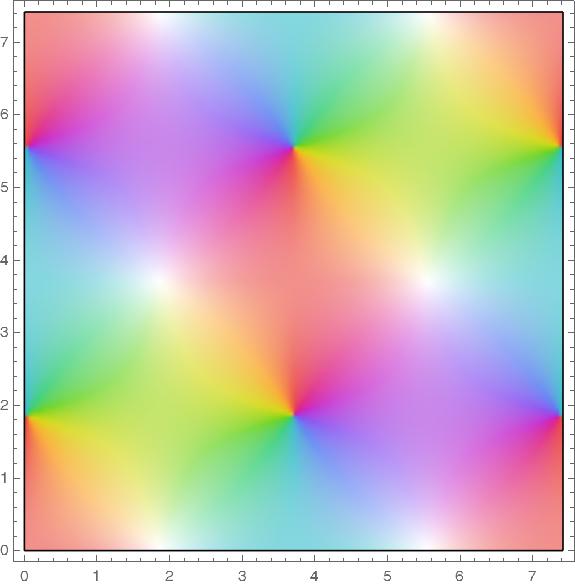
ds
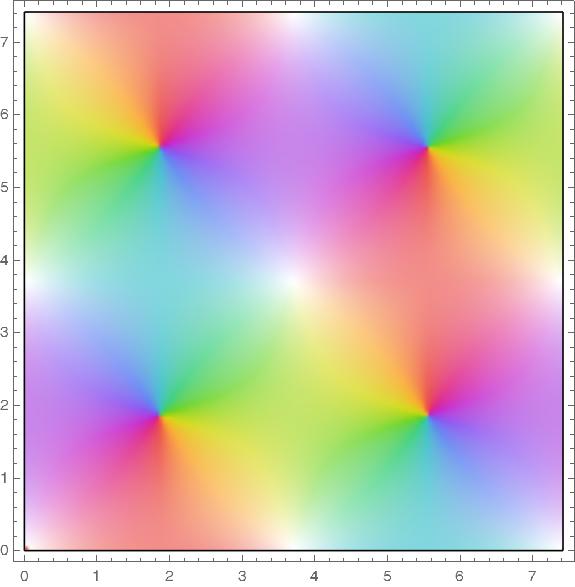
sd
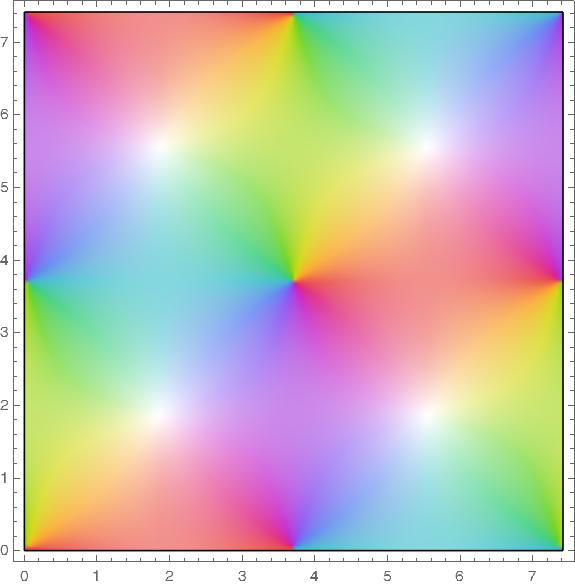
cs
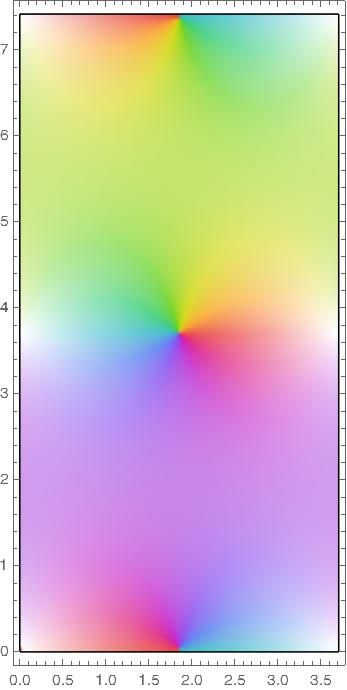
sc

dn
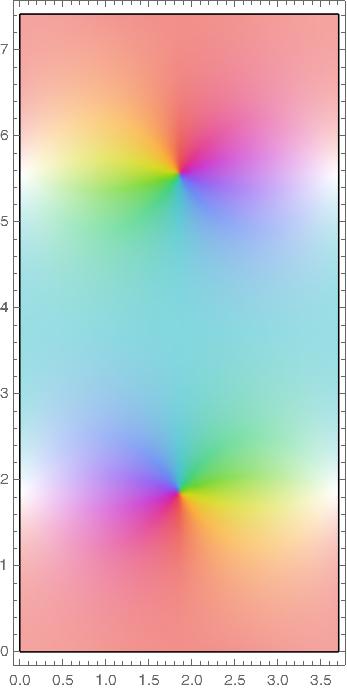
nd