There are many identities relating the values of the gamma function at one point to values at other points. These identities mostly derive from four basic identities. There are analogous identities for functions related to the gamma function — log gamma, digamma, trigamma, etc. — that follow the same pattern.
The diagram below helps to visualize the identity landscape.
- The conjugation identities all have the same form. They say conjugation commutes with function application.
- The addition identities relate the values of a function at z and z+n where n is an integer.
- The reflection identities relate values of a function at z and 1-z.
- The multiplication identities relate the value of a function at integer multiples of z to a sum or product of function applications at fractional shifts of z.
Table of Identities
The following table gives links to the specifics of each kind of identity.
| Gamma | Log gamma | Polygamma |
| conjugation | conjugation | conjugation |
| addition | addition | addition |
| reflection | reflection | reflection |
| multiplication | multiplication | multiplication |
The digamma function ψ(z) is the derivative of log Γ(z). The polygamma function ψ(n)(z) is the nth derivative of ψ(z) for integer n ≥ 1 and ψ(0)(z) = ψ(z).
References to A&S are formula numbers in Abramowitz and Stegun.
Gamma identities
Conjugation
![]()
A&S 6.1.23
Addition
The simplest case of the addition identity corresponds to n = 1.
![]()
A&S 6.1.15
Here is the general case for positive integer n.
![]()
A&S 6.1.16
Reflection
![]()
A&S 6.1.17
Multiplication
The simplest case of the multiplication identity is the duplication formula.
![]()
A&S 6.1.18
Here is the general case for positive integer n.
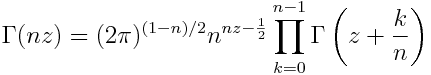
A&S 6.1.20
Log gamma identities
Conjugation
![]()
Take log of A&S 6.1.23
Addition
The simplest case of the addition identity corresponds to n = 1.
![]()
Take log of A&S 6.1.15
Here is the general case for positive integer n.
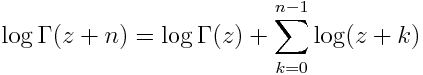
Take log of A&S 6.1.16
Reflection
![]()
Take log of A&S 6.1.17
Multiplication
The simplest case of the multiplication identity is the duplication formula.
![]()
Take log of A&S 6.1.18
Here is the general case for positive integer n.
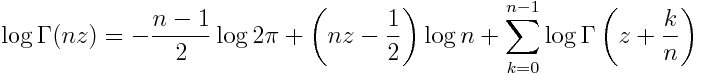
Take log of A&S 6.1.20
Polygamma identities
Conjugation
![]()
A&S 6.3.9
Addition
The simplest case of the addition identity corresponds to n = 1.
![]()
A&S 6.4.6
Here is the general case for positive integer n.
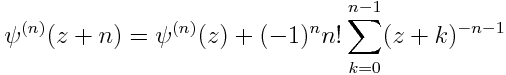
Iterate A&S 6.4.6
Reflection
![]()
A&S 6.4.7
Multiplication
The simplest case of the multiplication identity is the duplication formula. For the digamma function this is
![]()
A&S 6.4.8
For the polygamma function with n ≥ 1 the duplication formula is
![]()
For the digamma function, general multiplication formula for positive integer m is
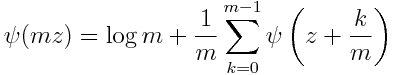
For the polygamma function with n ≥ 1 the multiplication formula is
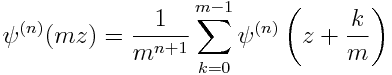
A&S 6.4.9
Other diagrams: See this page for more diagrams on this site including diagrams for probability and statistics, analysis, topology, and category theory.
