A knight’s tour magic square

Leonhard Euler created the following magic square.

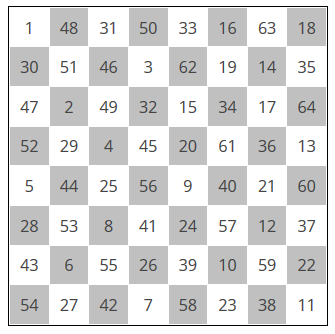
This magic square has three properties:

1. Each row and each column sums to 260.
2. Each half-row and each half-column sums to 130.
3. The sequence of squares containing 1, 2, 3, …, 64 form a knight’s tour.

The following Python code verifies that the magic square has the advertised properties.

# Euler's knight's tour magic square
a = [[ 1, 48, 31, 50, 33, 16, 63, 18],
     [30, 51, 46, 3, 62, 19, 14, 35],
     [47, 2, 49, 32, 15, 34, 17, 64],
     [52, 29, 4, 45, 20, 61, 36, 13],
     [ 5, 44, 25, 56, 9, 40, 21, 60],
     [28, 53, 8, 41, 24, 57, 12, 37],
     [43, 6, 55, 26, 39, 10, 59, 22],
     [54, 27, 42, 7, 58, 23, 38, 11]]

# Divide the chess board into four 4x4 blocks.
# Verify that in each block the rows and columns sum to 130.
# It follows that each entire row and entire column sums to 260.
for hblock in [0, 1]:
    for vblock in [0, 1]:
        for i in range(0,4):
            row_sum = col_sum = 0
            for j in range(0,4):
                row_sum += a[hblock*4 + i][vblock*4 + j]
                col_sum += a[hblock*4 + j][vblock*4 + i]
assert(row_sum == 130)
assert(col_sum == 130)

# Report whether it is legal for a knight to move from a to b.
def knight_move(a, b):
    return ((abs(a[0] - b[0]) == 2 and abs(a[1] - b[1]) == 1) or
            (abs(a[0] - b[0]) == 1 and abs(a[1] - b[1]) == 2))

# Map each square to its coordinates.
coordinate = {}
for row in range(0, 8):
    for col in range(0, 8):
        coordinate[ a[row][col] ] = (row, col)

# Verify that the sequence of numbers are legal knight moves.
for i in range(1, 64):
    assert knight_move( coordinate[i], coordinate[i+1] )

# If the script gets this far, no assertion failed.
print "All tests pass."