This page contains the math-related posts from my short-lived blog Symbolism. The non-mathematical posts are collected here.
Table of contents:
- Weierstrass p function
- Rotated T’s
- Cyrillic letters in math
- Planck’s constant
- Epi and mono arrows
- There exists
- Long S
- Equals
- Aleph
Weierstrass p function
Mathematicians don’t often change the style of letters to denote special functions, but the Weierstrass ℘ function is a notable exception. The symbol is described in Unicode as U+2118 (SCRIPT CAPITAL P). It has a named HTML entity ℘. The LaTeX for ℘ is \wp.
The mathematical significance of the Weierstrass ℘ function is that all elliptic functions can be expressed as rational functions of this function and its derivatives.
Rotated T’s
Logic uses a symbol that looks like a sans serif T (⊤, U+22A4) to denote “true.” The same symbol turned upside down (⊥, U+22A5) is used for “false.” An advantage of using this symbol rather than some form of F is that it makes the symmetry of some formulas more apparent.
Logic also uses symbols that look like a T rotated 90 ° clockwise or counterclockwise, ⊢ (U+22A2) and ⊣ (U+22A3). The expression x ⊢ y means that y is provable from x. Likewise x ⊣ y means that x is provable from y. Both expressions together are used for equivalence, i.e. x ⊣⊢ y means x and y are each provable from the other.
The symbols ⊢ (U+22A2) and ⊣ (U+22A3) are \vdash and \dashv in LaTeX.
The symbols ⊤ (U+22A4) and ⊥ (U+22A5) \top and \bot in LaTeX.
Cyrillic letters in math
I mentioned in a conversation that math rarely uses Hebrew or Russian letters. Andres Caicedo pointed out that the Cyrillic letter sha (Ш, U+0428) is an exception. It is used for the Tate–Shafarevich group of an Abelian variety. I’d never heard of such a thing before.
The letter sha is also used in distribution theory for the “Dirac comb,” an infinite sum of evenly spaced delta functions. I’d seen the Dirac comb before, but I don’t recall Ш being used as a symbol for it.
Sha is apparently an exception that proves the rule that Cyrillic letters are seldom used in math (at least in the West). Wikipedia says “Ш has the distinction of being the only distinctly Cyrillic letter internationally used in mathematics.” Also according to Wikipedia, sha probably comes form the modern Hebrew Shin letter (ש, U+05E9).
By the way, the phrase “the exception that proves the rule” doesn’t make sense as commonly interpreted. If anything, exceptions disprove a rule. I think the original understanding of the phrase was that if exceptions are remarkable, that shows that the rule often holds.
Planck’s constant
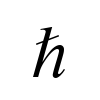In physics, Planck’s constant is the proportionality constant between energy and particle frequency: E = hν. When working with angular frequency ω = 2πν, it is convenient to introduce a new constant ħ equal to h/2π so that E = ħω. The symbol ħ is simply pronounced “h bar” and is sometimes called the reduced Planck constant.
The correct Unicode value for h is U+210E (PLANCK CONSTANT), not simply the common h U+0068 (LATIN SMALL LETTER H). Also, there is a character ħ in the Latin Extended-A portion of Unicode, U+0127 (LATIN SMALL LETTER H WITH STROKE), but the correct code point for ħ is U+210F (PLANCK CONSTANT OVER TWO PI). If you’re wondering why anyone should care about making such distinctions, see this post.
The LaTeX command for ħ is \hslash. LaTeX does not have a special command for h because it does not make semantic distinctions between visually identical characters.
If you look at the source for this page, you’ll see that I deliberately use the wrong characters for h and ħ. That’s because font support for Unicode is poor. I’m betting that more people will be able to see glyphs for the Latin letters than for the correct symbols.
Epi and mono arrows
Mathematicians sometimes decorate arrows in diagrams to encode more information about what the arrow represents. These decorations aren’t entirely standard, so it’s hard (at least for me) to remember what they mean.
One-to-one functions are denoted with an arrow with a split tail. This is U+21A3 or \rightarrowtail in LaTeX. (These are also called injective functions or monomorphisms.)
Onto functions are denoted with an arrow with two heads. This is U+21A0 or \twoheadrightarrow in LaTeX. (These are also called surjective functions or epimorphisms.)
I don’t know whether the following pattern was intentional, but it’s at least a mnemonic. If you know the meaning of the arrows above, you can use this to remember the category theory definitions. Or if you can remember the category theory definitions, you can use this to remember the meaning of the arrows.
In category theory, monomorphisms are defined using an diagram that has two arrows on the left. You could imagine these turning into the two lines in the tail of an arrow.
Epimorphisms are defined using a diagram with arrows on the right. You could imagine putting these two arrows on top of each other then sliding one horizontally so that you have two arrow heads.
There exists
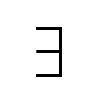In logic, a backward E is an abbreviation for “there exists.” The symbol is called the “existential quantifier.” Its code point in Unicode is U+2203. The TeX command to produce the symbol is \exists.
There are a couple common variations on the symbol. One is to follow the symbol by an exclamation point to denote that the thing whose existence is being asserted is unique, i.e. you can read the pair of symbols as “there exists a unique.”
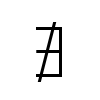Another variation is to draw a slash through the symbol to denote that something does not exist. The Unicode code point for this variation is U+2204 and the TeX command is \nexists.
Long S
Gottfried Leibniz used the initial ‘s’ of summa, the Latin for sum, to denote integration. He used a “long S,” a form of the letter commonly used in his day.
A famous example of the long S is the word “Congress” written atop the Bill of Rights.
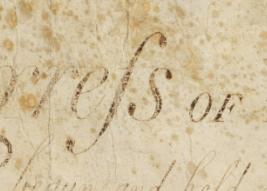
The long S fell out of use in print shortly after the Bill of Rights was written, though it persisted in handwriting a few decades longer.
The Unicode code point for the long S is U+017F. The code point for the integral sign is U+222B.
Equals
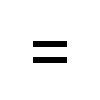It’s hard to imagine mathematics without an equal sign, but our symbol for equality was invented fairly recently relative to the history of mathematics. Robert Recorde invented the symbol in 1557 and it was not widely used until the 1700’s. Recorde used parallel lines to symbolize equality because “noe 2 thynges can be moare equalle.”
The meaning behind an equal sign can be subtle. We have to be careful about in what sense we consider the things on either side to be equal. Barry Mazur wrote a sophisticated article on this with the deceptively simple title When is one thing equal to some other thing?
Equality can be subtle in programming languages as well. The statement a = b can mean different things in different languages. In C it means to place the value b in the address a. In Python it means assign the name a to the value b. In C++, the assignment operator can be overloaded, and so a = b can cause arbitrary code to execute. In a functional programming language, a = b means to assign the value of b to a permanently. In other languages, it means that a contains or refers to the value b for now.
Aleph
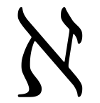The only Hebrew letter commonly used in mathematics is aleph, א, the first letter of the Hebrew alphabet. It is used with subscripts to denote the cardinality of various infinite sets. The most common use is with a subscript 0, pronounced “aleph naught” or “aleph null,” to denote the cardinality of the integers. The TeX command for aleph is, unsurprisingly, \aleph.
When used as a Hebrew letter, its Unicode code point is (U+05D0). When used as a mathematical symbol it has a distinct code point, U+2135. I expected aleph null (ℵ0) to have its own Unicode value but that doesn’t seem to be the case.
א is often transliterated aleph on the end; Wikipedia, for example, follows this convention. The Unicode standard, however, uses alef for the letter and many variations on it.
***
I’ve never used a Hebrew letter in HTML before writing this post and apparently there are things I need to learn about HTML and about WordPress. Here’s a little HTML file I created, entering the letter aleph three ways: as an HTML entity, using the Unicode value, and directly entering the letter:
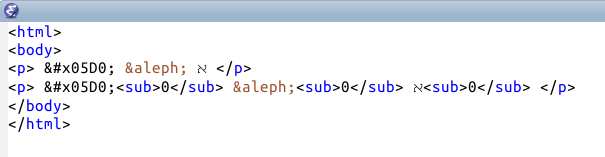
Here’s how this rendered in my browser:
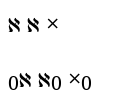
I’m surprised that entering HTML escape sequences for aleph produces different output than directly entering the aleph character. And I’m surprised that א<sub>0</sub> puts the subscript appears on the left but ℵ<sub>0</sub> puts the subscript on the right.
When I paste the same code into WordPress, this is what I see:
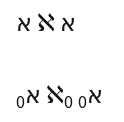
Now the escaped Unicode value and directly entering the character produce the same output, but the HTML entity ℵ produces a larger symbol. Also the subscript on the last item moved from the right side to the left side.
(The screenshots above were taken from Firefox running on Ubuntu. I get similar results on Windows using Firefox or Internet Explorer except that א and ℵ render in different fonts.)
Could someone please leave a comment explaining why the three different ways of entering an aleph use different fonts and follow different subscript rules? Thanks.
Update: I had assumed that the HTML entity ℵ was an abbreviation for the Hebrew letter aleph, but it is an abbreviation for the mathematical symbol aleph. This explains the different subscripting behavior. Also, thought that the default character set for HTML was UTF-8. But when I explicitly add <meta charset="UTF-8" /> to my HTML file I get the results I had expected, i.e. א and א work the same.