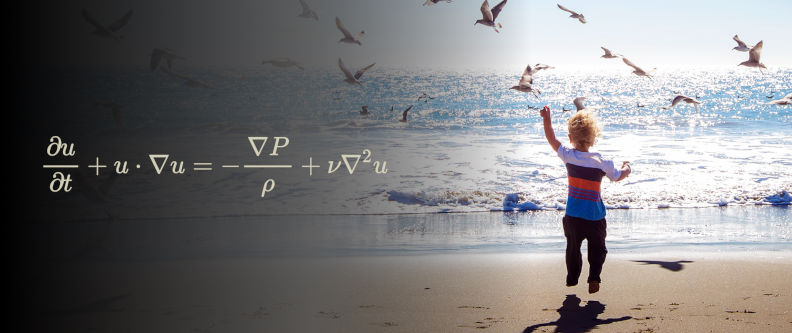
Differential equations have been around almost as long as derivatives. Shortly after people began computing derivatives and thinking about physical, practical problems in terms of derivatives, they realized how incredibly useful it would be to invert the process. Instead of needing to find the derivative of a known function, we often know equations the derivatives must satisfy and need to find the function.
So-called ordinary differential equations (ODEs) involve functions of one variable. Often that variable is time. Partial differential equations (PDEs) are more general, involving functions of several variables, such as several spatial variables or functions of space and time.
Boundary value problems
The hard part in working with differential equations, especially partial differential equations, is the boundary conditions. The differential equation itself is derived by examining what happens inside some system. Boundary conditions specify how that system interfaces with the rest of the world.
With ODEs the boundary may simply be a single point, time zero, in which case the boundary conditions are called initial conditions. With ODEs, the boundary conditions may specify the value of the solution or some of its derivatives on the boundary of some region of space, and may involve initial conditions as well.
Analytic and numerical solutions
In practice, solving differential equations almost always means producing numerical solutions. However, analytic solution methods remain important. An exact solution to a simplified problem, for example, can give you some assurance that your numerical solution is plausible. Also, some questions, such as stability and long-term behavior, may be easier to explore with analytic methods. When possible, it’s valuable to explore a differential equation model numerically and analytically.
Our background
Our president did his PhD and postdoc work in nonlinear PDEs. Others on our team have PhDs in statistics and computer science and have come to PDEs from their complementary perspectives. Together we have used differential equations to model complex systems in medical and financial applications.
Finding parameters with filtering
Not only is the solution to the differential equation initially unknown, but the exact form of the differential equation itself is unknown. Parameters are determined by a finite amount of empirical data, and so there is always some residual uncertainty regarding the exact values of the parameters.
The parameters may also vary over time, in which case you may have two kinds of simultaneous evolution: the PDE solution evolving over time while the parameters of the PDE itself are also evolving over time. In practice techniques such as Kalman filters or particle filters are used to update our knowledge of parameters as the differential equations evolve.
Our team has extensive experience in differential equations, statistics, and scientific computation. These all come together in solving differential equations and accounting for uncertainty in their parameters.
Help with modeling
If you’d like for me to help your company with differential equations, particle filtering, or other aspects of mathematical modeling, please call or email to discuss your project.
Trusted consultants to some of the world’s leading companies

