Spherical trigonometry is the study of curved triangles, triangles drawn on the surface of a sphere. The subject is practical, for example, because we live on a sphere. The subject has numerous elegant and unexpected theorems. We give a few below.
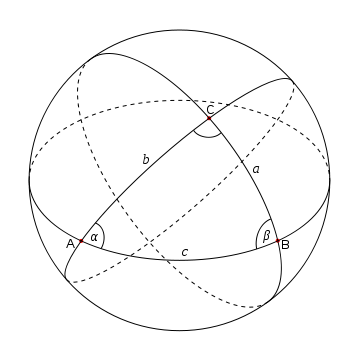
The diagram shows the spherical triangle with vertices A, B, and C. The angles at each vertex are denoted with Greek letters α, β, and γ. The arcs forming the sides of the triangle are labeled by the lower-case form of the letter labeling the opposite vertex.
Basic properties
On the plane, the sum of the interior angles of any triangle is exactly 180°. On a sphere, however, the corresponding sum is always greater than 180° but also less than 540°. That is, 180° < α + β + γ < 540° in the diagram above. The positive quantity E = α + β + γ − 180° is called the spherical excess of the triangle.
Since the sides of a spherical triangle are arcs, they can be described as angles, and so we have two kinds of angles:
- The angles at the vertices of the triangle, formed by the great circles intersecting at the vertices and denoted by Greek letters.
- The sides of the triangle, measured by the angle formed by the lines connecting the vertices to the center of the sphere and denoted by lower-case Roman letters.
The second kind of angle is most interesting. In contrast to plane trigonometry, the sides of a spherical triangle are themselves angles, and so we can take sines and cosines etc. of the sides as well as the vertex angles.
Right spherical triangles
For this section, assume the angle γ = 90°, i.e. we have a spherical right triangle. Then the following identities hold.
- sin a = sin α sin c = tan b cot β
- sin b = sin β sin c = tan a cot α
- cos α = cos a sin β = tan b cot c
- cos β = cos b sin α = tan a cot c
- cos c = cot α cot β = cos a cos b
Napier’s rule is a mnemonic for memorizing the above identities.
General spherical triangle
For this section we drop the assumption that γ = 90°. Many identities hold. Here are a few examples.
Law of sines
sin α / sin a = sin β / sin b = sin γ / sin c
Law of cosines
cos a = cos b cos c + sin b sin c cos α
cos α = -cos β cos γ + sin β sin γ cos a
Tangents
Let s = (a + b + c)/2 and let σ = (α + β + γ)/2. The following formulas can used to solve for a vertex angle from knowing the side arcs or solve for a side arc from knowing the vertex angle.
tan (α/2) = √( sin(s − b) sin(s − c) / sin s sin(s − a) )
tan (a /2) = √( −cos(σ) cos(σ − α) / cos(σ − β) cos(σ − γ) )
Area
Let R be the radius of the sphere on which a triangle resides. If angles are measured in radians, the area of a triangle is simply R2E where E is the spherical excess, defined above. In degrees the formula for area is πR2E/180.
