When I was in growing up, I had a copy of Handbook of Mathematical Tables and Formulas by R. S. Burington from 1940. When I first saw the book, much of it was mysterious. Now everything in the book is very familiar, and would be familiar to anyone who has gone through the typical college calculus sequence. But there is one exception: two pages on spherical trigonometry, the study of triangles drawn on a sphere.
Until recently, the only place I’d ever heard of spherical trig was Burington’s old book. I managed to find a book on spherical trig at the Rice University library, Spherical Trigonometry by J. H. D. Donnay, written in 1945. Amazon has several recent books on the spherical trig, but it appears they’re all reprints of much older books. It seems interest in teaching spherical trig died sometime after World War II.
I’m not sure why schools quit teaching spherical trig. It’s a practical subject; after all, we live on a sphere. Surveyors, navigators, and astronomers would find it useful. Somewhere along the way, solid geometry fell out of favor, and I suppose spherical trig fell out of favor with it. The standard math curriculum changed in order to make a bee line for calculus. Presumably this is to meet the needs of science and engineering students who need calculus as a prerequisite for their courses. In the process, subjects like solid geometry were squeezed out. I see the logic in the contemporary sequence, but it is interesting that the sequence was different a generation or two ago.
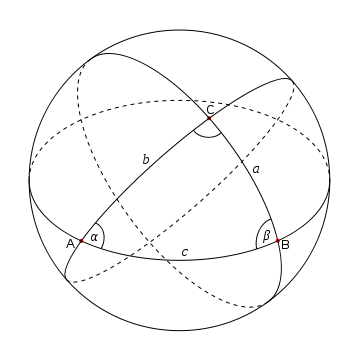
See Notes on Spherical Trigonometry for a list of some of the elegant identities from this now obscure area of math. For example, the interior angles of a spherical triangle must add up to more than 180°, and the area of the triangle is proportional to the amount by which the sum of these angles exceeds 180°.

I’ve been learning spherical triginometry in bits and pieces over the past year without knowing that that’s what it’s called. I took a job a year ago with a robotics company that makes UAVs. It’s amazing how large the error in your navigation calculations can grow when you try to ignore the curvature of the Earth. :)
Interesting … I always heard that before surveyors could demonstrate the curvature of the Earth by finding that the interior angles of a triangle on the surface added to more than 180 degrees, the vertices had to be on Himalayan mouintains, and even then it was dubious.
Here’s a guess — with WWII over and radar becoming more widely used, many fewer people needed to know old fashioned navigation. In the first place, there were a lot fewer night bomber sorties and covert reconnaisance flights. Those who did travel far could use radar as a much simpler and more accurate alternative, as it still is.
But I seriously doubt surveyors ever worried about the curvature of the Earth. First off, most surveying is done locally, and secondly local surface variation probably dwarfs any curvature effects.
As for astronomers, I don’t know, but it is not obvious to me why they would need it, unless it is simply beacuse they use spherical coordinates to locate things. And there aren’t that many of them, proportionally speaking.
Geographers and some map makers need to account for it, and the results at least need to be used for planning long range travel, but that still requires relatively few people to know how to do the calculations.
An interesting thing not many people know (present company excepted of course) is that the Earth was known to be a sphere at least since the ancient greeks, who even calculated the curvature using shadows of sticks. The old saw about Columbus having to convince Queen Isabella that the Earth was round instead of flat is a recent fiction. The controversy was over the distances involved in getting to East Asia by going West; Columbus had a radically optimistic opinion, which is why he assumed he had hit Asia when he hit the Americas.
Spherical trigonometry and the vector algebra of the unit sphere are both useful in applications involving directions, especially directions in 3D. There’s even a statistical subfield, typified by N.I.Fisher, T.Lewis, B.J.J.Embleton, STATISTICAL ANALYSIS OF SPHERICAL DATA, 1987.
As Bill the Lizard mentioned, the math mechanics of directions and such do get big billing in robotics work, too.
There is also hyperbolic trigonometry with its own sine and cosine laws.
This link is the best I can find on the web but it does little to emphasise the logical similarity to Euclidean trigonometry.
My math academic team is studying shperical trig. Is there someplace that I can find some practice questions? We only need problems that use the Law of Cos, Law of Sines , Napiers Circle and the area equation.
Evelyn, I’d look at the book by Donnay referenced in the post. It has been reprinted by Dover. Amazon lists several spherical trig books, all reprints of old books.
http://www.krysstal.com/sphertrig.html
This is a great website for spherical trig with exercises, etc.
Thanks for the link to krysstal.com. Looks good.
I am revisiting Spherical Trig after 30 years by going back over some of my books that I have collected over the years. Here are two that you may want to find.
1) on Amazon.com: Schaum’s Outline Series – Theory and Problems of Plane and Spherical Trigonometry by Frank Ayres, Jr. [1954 McGraw-Hill]
2)very old text book: Trigonometry For Home Study by William L. Schaaf
[1945 The New Home Library The Blakiston Company – Philadelphia]
I also have copies of sheets with 40+ problems and exercises I can share with anyone who is interested.
Also handy for direct exploration of spherical constructions: the spherical easel. http://merganser.math.gvsu.edu/easel/
I have my own hypothesis about why the standard biz analysis for an innovation turns out all wrong–geometry. A nascent tech startup with its own tech, not just whole product plays a Poisson game, so it’s underlying distribution in machine learning terms is about discovery, discovering a market. It is not a smooth linear Euclidean line.
As the company matures to a nice six sigma it the distribution becomes normal. I’ve actually seen this will real accounting data. The space becomes Euclidean, so the standard biz analysis works fine.
Once the company grows beyond six sigma, it moves into a spherical space where many linarites work. Information overload enables many different analyses to work, so all of the look Euclidean. Success abounds.
But when we applied our nice Euclidean analysis to the hyperbolic space, failure abounds.
Anyway, that’s my hypothesis.
Those other trigonometries are important even if we don’t teach them.
I’m suprised nobody mentioned celestial navigation as a practical application of spherical trigonometry. It is required to determine your location. One can’t simply use tables that have done all the calculations for you or use law of sines and cosines for spherical trigonometry and do the calculations yourself.