Suppose you have a radio transmitter T and a receiver R with a clear line of sight between them. Some portion the signal received at R will come straight from T. But some portion will have bounced off some obstacle, such as the ground.
The reflected radio waves will take a longer path than the waves that traveled straight from T to R. The worst case for reception is when the waves traveling a longer path arrive half a period later, i.e. 180° out of phase, canceling out part of the signal that was received directly.
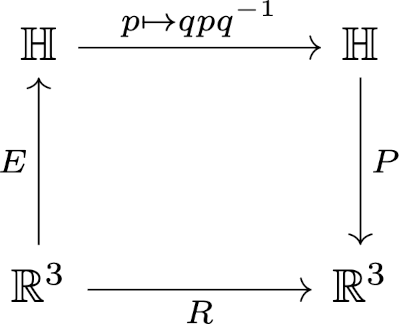
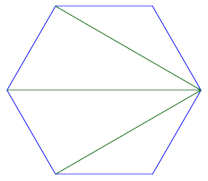
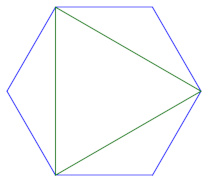
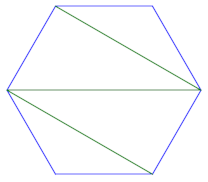
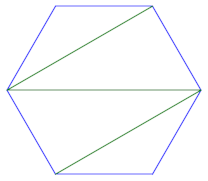
We’d like to describe the region of space that needs to be empty in order to eliminate destructive interference, i.e. signals 180° out of phase. Suppose T and R are a distance d apart and the wavelength of your signal is λ. An obstacle at a location P can cause signals to arrive exactly out of phase if the distance from T to P plus the distance from P to R is d + λ/2.
So we’re looking for the set of all points such that the sum of their distances to fixes points is a constant. This is the nails-and-string description of an ellipse, where the nails are a distance d apart and the string has length d + λ/2.
That would be a description of the region if we were limited to a plane, such as a plane perpendicular to the ground and containing the transmitter and receiver. But signals could reflect off an obstacle that’s outside this plane. So now we need to imagine being able to move the string in three dimensions. We still get all the points we’d get if we were restricted to a plane, but we also get their rotation about the axis running between T and R.
The region we’re describing is an ellipsoid, known as a Fresnel ellipsoid or Fresnel zone.
Suppose we choose our coordinates so that our transmitter T is located at (0, 0, h) and our receiver R is located at (d, 0, h). We imagine a string of length d + λ/2 with endpoints attached to T and R. We stretch the string so it consists of two straight segments. The set of all possible corners in the string traces out the Fresnel ellipsoid.
Greater delays
If reflected waves are delayed by exactly one period, they reinforce the portion of the signal that arrived directly. Signals delayed by an even multiple of a half-period cause constructive interference, but signals delayed by odd multiples of a half-period cause destructive interference. The odd multiples matter most because we’re more often looking to avoid destructive interference rather than seeking out opportunities for constructive interference.
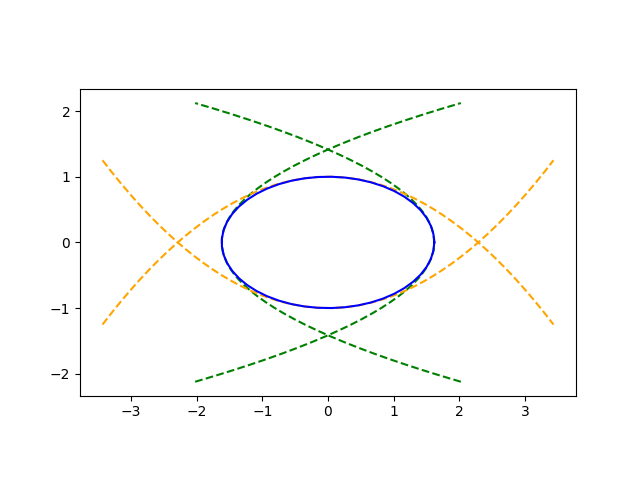
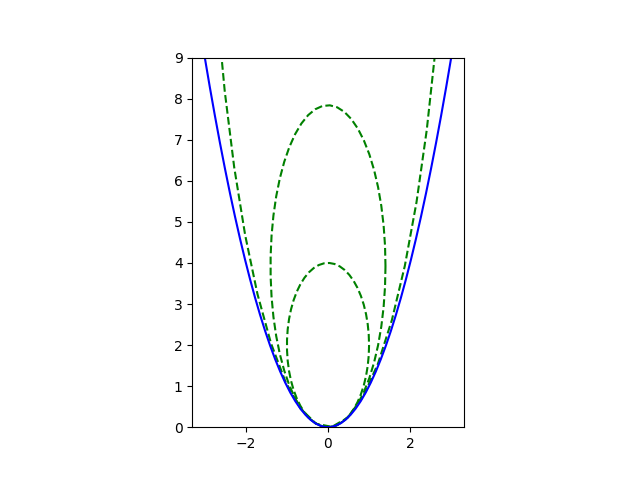
If you repeat the exercise above with a string of length length d + λ you have another Fresnel ellipsoid. The foci remain the same, i.e. T and R, but this new ellipsoid is bigger since the string is longer. This ellipsoid represents locations where a signal reflected at that point will arrive one period later than a signal traveling straight. Obstacles on the surface of this ellipsoid cause constructive interference.
We can repeat this exercise for a string of length d + nλ/2, where odd values of n correspond to regions of destructive interference. This gives us a set of confocal ellipsoids known as the Fresnel ellipsoids.