Draw a few points on a circle and then draw a straight line from every point to every other point. Count the number of regions created.
2 points, 2 regions.
3 points, 4 regions.
4 points, 8 regions.
5 points, 16 regions.
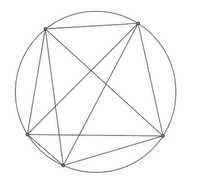
6 points? See this post from the f(t) blog for the answer.
{ 12 comments… read them below or add one }
John Venier 04.22.09 at 11:38
You bring up a fascinating philosophical question — the problem of induction, one of the great problems of (at least Western) philosophy. I think it is fascinating because there is no way to reason from first principles that inductive reasoning should apply, and yet all of science (by which I mean the experimental variety, as opposed to theoretical) relies on it utterly. Moreover we all personally depend on it constantly, and life or existence without being able to rely on it is difficult to imagine. It is also the basis for eliciting prior information in Bayesian statistics.
I suspect the answer to this riddle is deep indeed.
Besides being an example where inductive reasoning fails, your observation is a good example of why I hate the “What’s the next (or missing) value in the sequence of integers?” puzzles, or problems on IQ tests. They are of course incorrigably ill-posed problems, except perhaps trivially by supplying the answer while posing the problem, or constraining the possible answers so that only one number fits the constraints. Anyway, while they can be constructed to minimize the difficulty in most cases, sometimes the constructor does not even know that there is a difficulty. This seems especially the case in elementary school work.
Kate Nowak 04.22.09 at 12:46
I thought that at one time I sat through a rigorous proof of why proof by induction was valid. Like in an undergrad number theory class. I could be mistaken though.
John 04.22.09 at 13:08
The problem here isn’t induction in the mathematical sense. It’s an example of induction in the colloquial sense of extrapolating a pattern based on tuition.
Say we conjecture that n points leads to 2^(n-1) regions. A rigorous mathematical proof would establish the theorem for a base case, say n = 2. Next it would prove that if the theorem holds for any m >= 2 then it also holds for m+1. But in this case, the inductive step isn’t true and so it cannot be proven and neither can our conjecture.
John Venier 04.22.09 at 13:09
Well sure, what’s called “proof by induction” in math is fine.
The kind of induction I was writing about is concluding that because you have cracked open 100 eggs and seen a yolk inside, the next one you crack open will have a yolk inside.
Unfortunately I don’t have a broad enough vocabulary to know a term that distinguishes this reasoning from mathematical induction. Similarly, although I could write that there is no logical reason to believe the 101st egg will have a yolk inside it (and this is true) some folks would read “logical” as “sensible” and come to the opposite conclusion.
For some reason I find it difficult to discuss — probably my paucity of terms with unambiguous meanings. Also, inductive reasoning is so ingrained our consciousness, science, even the behavior of living organisms (in as much as they can be held capable of belief, expectation, or reasoning; if anthropomorphised their behavior clearly reflects it) that it is difficult to percieve it itself. This means that unless someone has thought about it previously, they are unlikely to be persuaded in a short conversation that it is different from deductive reasoning, present company excluded of course
John 04.22.09 at 13:15
JV: I agree with your skepticism regarding test questions of the form “What number is next in this sequence?” I hated those questions in school. I wanted to justify my answer, which of course you can’t do on a multiple choice test on a bubble form. If I were grading such an exam, I would reward someone who could give a good defense for an unusual answer. Of course standardized tests punish such original thought.
John Venier 04.22.09 at 13:17
[N.B. This and my previous comment are directed primarly at Kate Nowak, even though it looks like I am commenting incoherently on John's comment
]
Maybe this article will help. I haven’t read it thoroughly but it seems to be on the right track. Note in particular the bit at the end about mathematical induction.
John Venier 04.22.09 at 13:29
John: Absolutely. I think that the only reasonable way to ask those number-seuqence problems is to treat them like essay questions, where the quality of your argument is being assessed rather than the conclusion you draw. When you get down to it, the number-sequence problems are asking an opinion, like what the best ice cream flavor is. In that case most folks would get the right answer if the choices were appropriately limited, even though in principle there is no one correct answer.
John Venier 04.22.09 at 13:39
Hey John, you were wondering a while back about a better term than Bayesian for Bayesian statistics. How about referring to frequentist statistics as ‘deductive statistics’ and Bayesian statsitics as ‘inductive statistics’
Peter Turney 09.09.09 at 08:35
The two types of induction are sometimes called mathematical induction and statistical induction. There are several types of mathematical induction (weak induction, strong induction, transfinite induction, etc.) and all of them are special types of deductive reasoning. Statistical induction is not deductive. Often types of reasoning are carved up into four classes: deductive, inductive, abductive, and analogical. See:
http://plato.stanford.edu/entries/induction-problem/
http://en.wikipedia.org/wiki/Mathematical_induction
http://en.wikipedia.org/wiki/Inductive_reasoning
http://en.wikipedia.org/wiki/Deductive_reasoning
http://en.wikipedia.org/wiki/Abductive_reasoning
http://en.wikipedia.org/wiki/Analogical_reasoning
It can be argued that inductive, deductive, and abductive reasoning are all based on a foundation of analogical reasoning:
http://www.jfsowa.com/pubs/analog.htm
John V. 09.09.09 at 09:46
Thanks Peter!
It reminds me of what I am told regarding the Syadvada system of Jain logic, where there are seven logical states: true, false, true or false, indeterminate, true or indeterminate, false or indeterminate, true or false or indeterminate.
We tend to assume that ways of thinking which seem fundamental to us are universal. From what I can tell, this is far from accurate.
I was told that a certain evangelical organization contracted with the Gallup organization to prove that regardless of particular religion or culture, most people believe in some kind of God. The evangelicals knew this to be true, but wanted evidence to present to skeptics. The Gallup folks polled the Japanese, and found that a majority didn’t believe in any sort of God.
Peter Turney 09.09.09 at 10:02
There are many varieties of multi-valued logic:
http://en.wikipedia.org/wiki/Multi-valued_logic
Multi-valued logics are all types of deductive logic. Other types of deductive logic are temporal or tense logic (the logic of time — and there are many different logics of time), modal logic (the logic of possibility and necessity — and there are many different modal logics), intuitionist logic (denies the law of the excluded middle), relevance logic (the logic of relevant implication — many varieties), and so on.
John V. 09.09.09 at 10:18
Fascinating! In classical Hindu philosophy they likewise have eight or so methods of proof, IIRC.
When I was a kid I tried to construct a three-valued logic system for a science fiction story I was writing. One of the hypotheses for the story was that we (as humans) use two-valued logic and generally binary ways of thinking because we are bilaterally symmetric. Assuming that, I wondered, how would sentient beings who were trilaretally symmetric construct their understanding of the world? I decided to call the truth states red, yellow, and blue to avoid bias. I was merrily constructing logical operation tables when I heard that this had already been done, for arbitrary (n) values of truth. I lost interest after that.
I guess the philosophy of logic is much deeper and broader than I thought!