My previous post looked at rolling 5 six-sided dice as an approximation of a normal distribution. If you wanted a better approximation, you could roll dice with more sides, or you could roll more dice. Which helps more?
Whether you double the number of sides per die or double the number of dice, you have the same total number of spots possible. But which approach helps more? Here’s a plot.
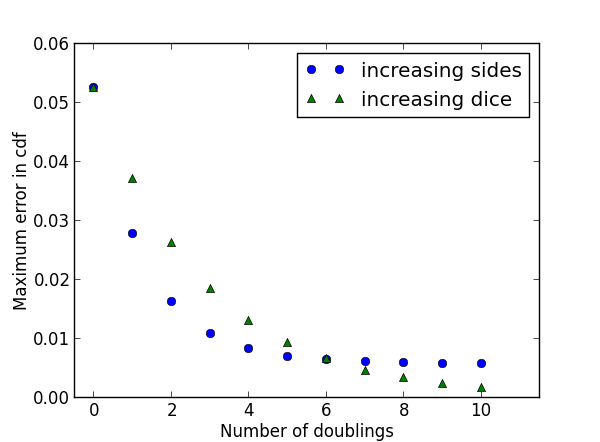
We start with 5 six-sided dice and either double the number of sides per die (the blue dots) or double the number of dice (the green triangles). When the number of sides n gets big, it’s easier to think of a spinner with n equally likely stopping points than an n-sided die.
At first, increasing the number of sides per die reduces the maximum error more than the same increase in the number of dice. But after doubling six times, i.e. increasing by a factor of 64, both approaches have the same error. But further increasing the number of sides per die makes little difference, while continuing to increase the number of dice decreases the error.
The long-term advantage goes to increasing the number of dice. By the central limit theorem, the error will approach zero as the number of dice increases. But with a fixed number of dice, increasing the number of sides only makes each die a better approximation to a uniform distribution. In the limit, your sum approximates a normal distribution no better or worse than the sum of five uniform distributions.
But in the near term, increasing the number of sides helps more than adding more dice. The central limit theorem may guide you to the right answer eventually, but it might mislead you at first.

What happens if you both increase the number of sides and number of dice?
Also, despite being a gamer, I’ve never seen a dice with more then 100 sides, and even then it is a pain to use. A 384 (6*64) sided die would simply be a pain to use due to the size of the sides or the size of the die. That and I’m not even sure how you would build it.
Yes, I know you can very easily pick a number out of a hat, or use a computer or such, but where is the fun in that?
This was really interesting. Is there a plain-language way to explain the “why” of this, or is it something that is hard to simplify much more than your (already well-done) post?
Look at the extreme case. Suppose you had a die with so many faces that you effectively have a continuous random variable, say a trillion faces. A roll of such a die is still just one sample from a uniform random variable.
Now consider the other extreme, one ordinary die and a trillion rolls. The central limit theorem says the total number of spots is effectively normal.
Thanks, that helps with perspective.