If you write out a sequence of Fibonacci numbers, you can see that the last digits repeat every 60 numbers.
The 61st Fibonacci number is 2504730781961. The 62nd is 4052739537881. Since these end in 1 and 1, the 63rd Fibonacci number must end in 2, etc. and so the pattern starts over.
It’s not obvious that the cycle should have length 60, but it is fairly easy to see that there must be a cycle. There are only 10*10 possibilities for two consecutive digits. Since the Fibonacci numbers are determined by a two-term recurrence, and since the last digit of a sum is determined by the sum of the last digits, the sequence of last digits must repeat eventually. Here “eventually” means after at most 10*10 terms.
Replace “10” by any other base in the paragraph above to show that the sequence of last digits must be cyclic in any base. In base 16, for example, the period is 24. In hexadecimal notation the 25th Fibonacci number is 12511 and the 26th is 1DA31, so the 27th must end in 2, etc.
Here’s a little Python code to find the period of the last digits of Fibonacci numbers working in any base b.
from sympy import fibonacci as f
def period(b):
for i in range(1, b*b+1):
if f(i)%b == 0 and f(i+1)%b == 1:
return(i)
This shows that in base 100 the period is 300. So in base 10 the last two digits repeat every 300 terms.
The period seems to vary erratically with base as shown in the graph below.
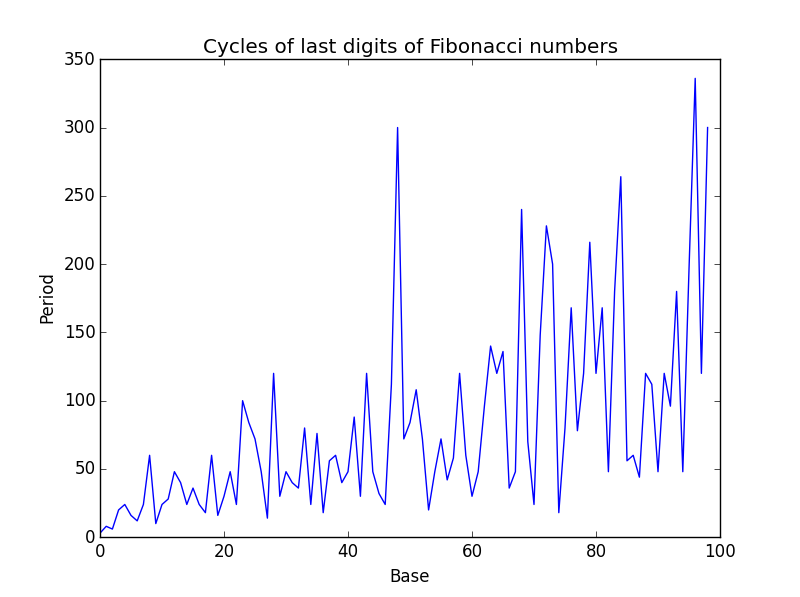
Related: Applied number theory

But the cycle doesn’t have to go through 0 and 1, right? But apparently it does for all the bases up to a 100?
What does the graph look like if you divide by the base?
It’s in OEIS (but only recently): https://oeis.org/A213278
I believe you can apply the recurrence relation backward to show that the cycle does have to go through 0 and 1.
I’m without a computer at the moment but I do wonder: which 2 digit sequences do not appear? There must be some as only 61 distinct pairs appear in the entire Fibonacci sequence.
Bootvis: Here are the sequences that do appear.
0 1
0 3
0 7
0 9
1 0
1 1
1 2
1 4
1 5
1 6
1 7
1 9
2 3
2 5
2 7
2 9
3 0
3 1
3 2
3 3
3 5
3 6
3 7
3 8
4 1
4 3
4 5
4 9
5 1
5 2
5 3
5 4
5 6
5 7
5 8
5 9
6 1
6 5
6 7
6 9
7 0
7 2
7 3
7 4
7 5
7 7
7 8
7 9
8 1
8 3
8 5
8 7
9 0
9 1
9 3
9 4
9 5
9 6
9 8
9 9
So all the even sequences are missing, and these 15:
2 1
4 7
6 3
8 9
9 2
3 4
7 6
1 8
1 3
3 9
7 1
9 7
0 5
5 0
5 5
Thanks Sjoerd! Too bad there is no obvious pattern here.
Could I be so bold as to say that I don’t expect there to be a ‘pattern’ or rather I expect it to be iid since the Fibonacci constant (handwaves Polya) is (handwaves some Erdos more) irrational?
Since you can start at any random pair and apply the recursion formula, and because, as John said, you can apply the recurrence relation backward, each pair belongs to some cycle, and you get permutation groups of pairs modulo n. Here are the permutations for n from 1 to 8:
(Using a variation on cyclic notation where (abc) really means (a b, b c, c a))
1: (0)
2: (0)(011)
3: (0)(01120221)
4: (0)(011231)(022)(033213)
5: (0)(01123033140443202241)(1342)
6: (0)(011235213415055431453251)(02240442)(033)
7: (0)(0112351606654261)(0224632505531452)(0336213404415643)
8: (0)(011235055271)(022462)(033617077653)(044)(066426)(134732574372)(145167541563)
The number of cycles is http://oeis.org/A015134, and for n=10 it gives 6 cycles, which we can check:
(0)(0112358… the cycle of 60 long …)(02246066280886404482)(2684)(134718976392)(055)
Dear Dr. Cook,
I am a retired math teacher and noticed that F(15n) always ends in 0, and is preceded by (and of course followed by) a number whose unit digit is:
1 for n = 4,8,12,…4k+4
3 for n = 3,7,11,…4k+3
7 for n = 1,5,9.,..4k+1
9 for n=2,6,10,…4k+2
The pattern 7,9,3,1 repeats.
The numbers 1, 3, 7, and 9 have an interesting property in that for each of them, when we multiply by the digits 0 – 9 , the unit digits are unique. I enjoyed the posts! -Jim
There IS a pattern to the last digits of the Fibonacci sequence, in fact, if you divide the 60 terms into 4 columns ( reading from up to down), you get:
1793
1793
2486
3179
5555
8624
3179
1793
4862
5555
9317
4862
3179
7931
0000
There are 8 rows that consists of the terms 1793
There are 4 rows that consists of the terms 2486
There are 3 rows that consists of only 5’s
There is one row of 0’s.
Each row adds up to 20 (other than the one with 0’s)
You can get 10 ordered pairs from each adjacent term (for example, 2 and 4 or 7 and 9). I graphed it and got perfect square with side lengths of 2*sqrt(10) – not including the ordered pairs (5,5) or (0,0).
I got excited when I saw 3145…. in rows 5, 6, and 7, and I tried to find how pi could fit into the sequence, but failed to find any terms of pi that coincided with the sequence.
I acquired all this information, but I have absolutely no idea how to apply it. I am currently in Geometry (Middle school) so I don’t have any experience with Number Theory or whatever math course that is needed to apply this info. Please add on to my thoughts as I am curious to see what other mathmeticians think! (To any of you wondering WHY a middle schooler would indulge in such hard math, it is because a friend of mine said that her phone password was the first digits of pi. I wanted a new phone password, and I wanted it to be long, but easy to find out if you knew the concept. So, I decided to use the last digits of the Fibonacci sequence and I got carried off …. :D )
Cool topic.
It does seem erratic, but on a larger scale, some simple straight lines appear.
https://repl.it/@prof_pantaloni/cycle-length-for-Fibonacci-mod-n
Dr. Cook-
Is there any information available regarding likelihood of next digit given a particular digit of random Fn?
How about for next digit in 5^.5?
How would I explore this is a spreadsheet?
Thanks for any help.
Kind regards.
-Sean