Relations between special functions
The diagram below illustrates the relationships between many common special functions.
The hypergeometric functon 2F1 has many special cases. (See these notes on hypergeometric functions for definitions and notation.)
The Jacobi polynomials are related to 2F1 by
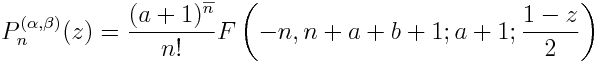
Jacobi polynomials with α = β are called Gegenbauer or ultraspherical polynomials and are denoted C(α)n. The Legendre polynomials Pn are Gegenbauer polynomials with α = 0. The Chebyshev polynomials of the first kind Tn are Gegenbauer polynomials with α = -½. The Chebyshev polynomials of the second kind Un are Gegenbauer polynomials with α = ½.
The incomplete beta function Bx(a, b) is related to 2F1(x) by
![]()
The beta function B(a,b) is defined to be Γ(a) Γ(b) / Γ(a+b) and equals B1(a, b).
The complete elliptic integrals K(z) and E(z) are related to 2F1 by
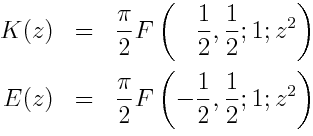
The complete elliptic integrals are the values of the incomplete elliptic integrals F(φ, z) and E(φ, z) at φ = φ/2.
The inverse of the integral F(φ, z) is the Jacobi elliptic function sn. The Jacobi functions sn, cn, and dn are intimately related, much like the elementary trigonometric functions.
The hypergeometric functon 1F1 is also known as the confluent hypergeometric function. It is related to the hypergeometric function 2F1 by
![]()
The incomplete gamma function γ(a, z) is related to 1F1 by
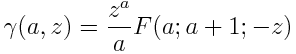
The limit of γ(a, z) as z goes to infinity is the gamma function Γ(a).
The derivative of the logarithm of the gamma function Γ(z) is the function ψ(z).
The error function erf(z) is related to 1F1 by
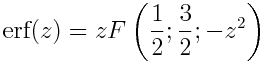
The error function erf(z) is related to the Fresnel integrals C(z) and S(z) by
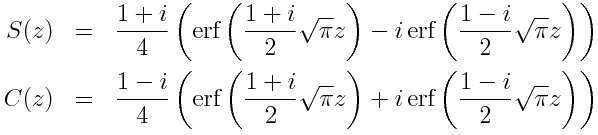
The Laguerre polynomials Lαn are related to 1F1 by
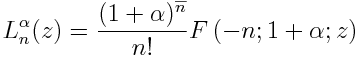
The Hermite polynomials are related to the Laguerre polynomials by
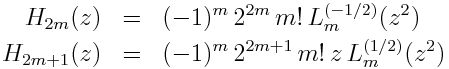
The hypergeometric functon 0F1 is related to the hypergeometric function 1F1 by
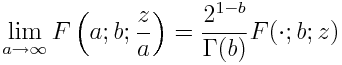
Only Bessel functions of the first kind Jν are shown on the diagram. Other Bessel functions are related to Jν as described here.
Other diagrams on this site
See this page for more diagrams on this site including diagrams for probability and statistics, analysis, topology, and category theory.
