If a real polynomial in one variable is a sum of squares, it obviously cannot be negative. For example, the polynomial
p(x) = (x2 – 3)2 + (x + 7)2
is obviously never negative for real values of x. What about the converse: If a real polynomial is never negative, is it a sum of squares? Yes, indeed it is.
What about polynomials in two variables? There the answer is no. David Hilbert (1862–1943) knew that there must be positive polynomials that are not a sum of squares, but no one produced a specific example until Theodove Motzkin in 1967. His polynomial
p(x, y) = 1 – 3x2y2 + x2 y4 + x4 y2
is never negative but cannot be written as a sum of any number of squares. Here’s a plot:
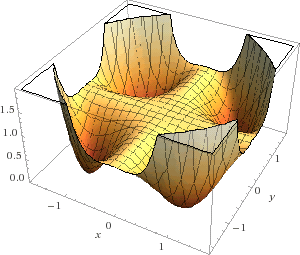
Source: Single Digits

How about an easier problem? Can there be a n-variable polynomial that is positive and surjective, sending R^n onto (0,\infty)? Someone posted this on a board a couple weeks ago, and an answer was quickly provided. Note Motzkin’s has p(1,1)=0.
It is a sum of squares, but you have to use rational functions instead of polynomials. In that case, the converse is true. This is Hilbert’s 17th problem, which was solved by Artin in 1927 http://en.wikipedia.org/wiki/Hilbert%27s_seventeenth_problem
@Aaron perhaps you could demonstrate these rational functions using sympy? I have a hard time “visualizing” this.
As far as I know, SymPy doesn’t have any algorithms for computing this. I’m not even sure what the sum of squares form of Motzkin’s polynomial is.
The way to think of this is that for real polynomials, there is only one inequality, x^2 >= 0. All other inequalities are reducible to this form (subtract everything to the greater than side, rewrite the expression as a sum of squares).
See for instance https://andrescaicedo.wordpress.com/2008/11/11/275-positive-polynomials/, which shows some famous inequalities (AM-GM and Cauchy-Shwarz) in this way.
If I recall there are some nice ways to produce a sum of squares, if one exists at all, using semidefinite programs. You can reformulate f being a sum of squares as f = z^T A z for some positive semidefinite matrix A, where z is the vector of all monomials of degree <= d and deg(f) = 2d. If we can find such an A, then the eigendecomposition of A gives us the sum of squares representation of f. Finding such an A is a semidefinite program, which can be solved numerically often.