Numerically integrating periodic functions

The trapezoid rule is the most obvious numerical integration technique. It comes directly from the definition of a definite integral, just a Riemann sum.

It’s a very crude technique in general; you can get much more accuracy with the same number of function evaluations by using a more sophisticated method. But for smooth periodic functions, the trapezoid rule works astonishingly well.

This post will look at two similar functions. The trapezoid rule will be very accurate for one but not for the other. The first function is

g(x) = exp( cos(x) ).

The second function, h(x) replaces the cosine with its Taylor approximation 1 – x²/2. That is,

h(x) = exp(1 – x²/2 ).

The graph below shows both functions.

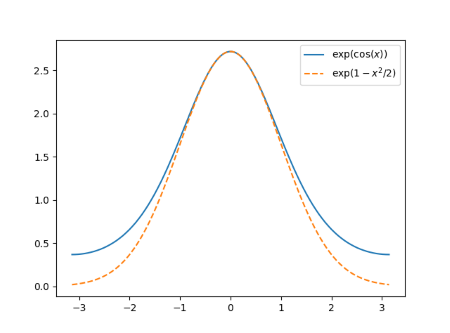
Both functions are perfectly smooth. The function g is naturally periodic with period 2π. The function h could be modified to be a periodic function with the same period since h(-π) = h(π).

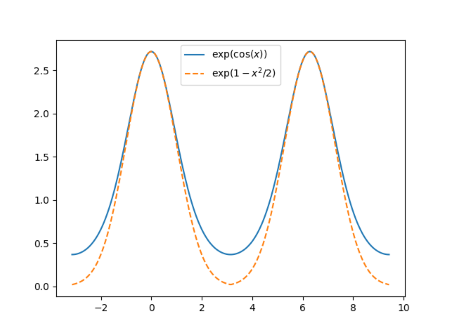
But the periodic extension of h is not smooth. It’s continuous, but it has a kink at odd multiples of π. The derivative is not continuous at these points. Here’s a close-up to show the kink.

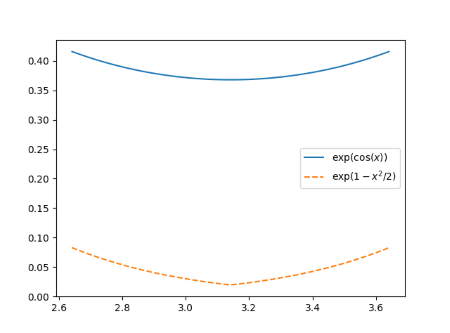
Now suppose we want to integrate both functions from -π to π. Over that range both functions are smooth. But the behavior of h “off stage” effects the efficiency of the trapezoid rule. Making h periodic by pasting copies together that don’t match up smoothly does not make it act like a smooth periodic function as far as integration is concerned.

Here’s the error in the numerical integration using 2, 3, 4, …, 10 integration points.

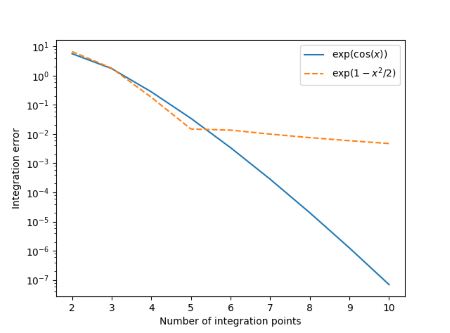
The integration error for both functions decreases rapidly as we go from 2 to 5 integration points. And in fact the integration error for h is slightly less than that for g with 5 integration points. But the convergence for h practically stops at that point compared to g where the integration error decreases exponentially. Using only 10 integration points, the error has dropped to approximately 7×10^-8 while the error for h is five orders of magnitude larger.

To read more along these lines, see J. A. C. Weideman’s article Numerical Integration of Periodic Functions: A Few Examples, The American Mathematical Monthly, Vol. 109, No. 1, pp. 21–36.