Since integration is the inverse of differentiation, you can think of integration as “dividing” by d.
J. P. Ballantine [1] shows that you can formally divide by d and get the correct integral. For example, he arrives at
using long division!
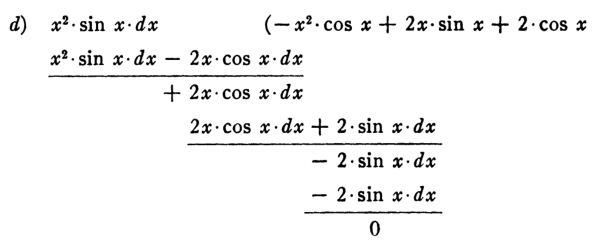
[1] J. P. Ballantine. Integration by Long Division. The American Mathematical Monthly, Vol. 58, No. 2 (Feb., 1951), pp. 104-105

John – isn’t this just tabular integration by parts written in a slightly different form?
This is reminiscent in its way of Oliver Heaviside’s Operator Calculus, where he blithely multiplied and divided his operators — even raising them to fractional powers — and happily manipulated divergent series, all while revolutionizing how electrical systems were analyzed. Personally he showed many signs of being a crank, with remarkable disdain for those who carefully explained why “you can’t just do that.” Although he enjoyed remarkable success (for his time) I’m glad I was able to use Laplace transforms when I was an E.E. undergrad.
https://deadreckonings.com/2007/12/07/heavisides-operator-calculus/
The method of long division works for solving any system Ax = b for x, where:
1) A is a linear operator (in more familiar forms of long division, this is multiplication by a real number or polynomial), acting on a vector space of which b is an element, and
2) you have some method of choosing y such that Ay = b + r, reducing the problem of solving Ax = b to the problem of solving Ay = r. Long division is just a notation for iterating this process. Of course, for this to do anything meaningful, r has to be “smaller” than b in some way. For long division of real numbers, we choose y such that r < b as numbers; for long division of polynomials, we choose y such that r has a lower degree than b.
What I don't understand here is how we choose y in general. In this case (and many other integration by parts cases) there is an easy choice of y that works because we are reducing the power of x in the integral, but is there some more general way to choose y?