Higher dimensional squircles

The previous post looked at what exponent makes the area of a squircle midway between the area of a square and circle of the same radius. We could ask the analogous question in three dimensions, or in any dimension.

(What do you call a shape between a cube and a sphere? A cuere? A sphube?)

 

In more conventional mathematical terminology, higher dimensional squircles are balls under L^p norms. The unit ball in n dimensions under the L^p norm has volume

We’re asking to solve for p so the volume of a p-norm ball is midway between that of 2-norm ball and an ∞-norm ball. We can compute this with the following Mathematica code.

    v[p_, n_] := 2^n Gamma[1 + 1/p]^n / Gamma[1 + n/p]
    Table[ 
        FindRoot[
            v[p, n] - (2^n + v[2, n])/2, 
            {p, 3}
        ], 
        {n, 2, 10}
    ]

This shows that the value of p increases steadily with dimension:

    3.16204
    3.43184
    3.81881
    4.33311
    4.96873
    5.70408
    6.51057
    7.36177
    8.23809

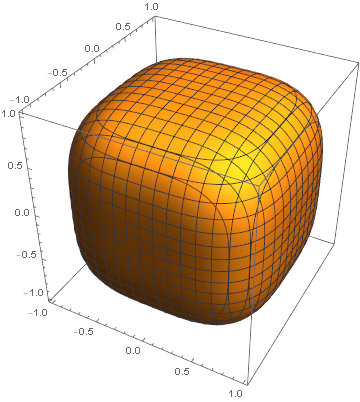
We saw the value 3.16204 in the previous post. The result for three dimensions is 3.43184, etc. The image above uses the solution for n = 3, and so it has volume halfway between that of a sphere and a cube.

In order to keep the total volume midway between that of a cube and a sphere, p has to increase with dimension, making each 2-D cross section more and more like a square.

Here’s the Mathematica code to draw the cuere/sphube.

    p = 3.43184
    ContourPlot3D[
         Abs[x]^p + Abs[y]^p + Abs[z]^p == 1, 
         {x, -1, 1}, 
         {y, -1, 1}, 
         {z, -1, 1}
    ]