I recently had to work with the function
f(x; k) = arctan( k tan(x) )
The semicolon between x and k is meant to imply that we’re thinking of x as the argument and k as a parameter.
This function is an example of the coming full circle theme I’ve written about several times. Here’s how a novice, a journeyman, and an expert might approach studying our function.
- Novice: arctan( k tan(x) ) = kx.
- Journeyman: You can’t do that!
- Expert: arctan( k tan(x) ) ≈ kx for small x.
Novices often move symbols around without thinking about their meaning, and so someone might pull the k outside (why not?) and notice that arctan( tan(x) ) = x.
Someone with a budding mathematical conscience might conclude that since our function is nonlinear in x and in k that there’s not much that can be said without more work.
Someone with more experience might see that both tan(x) and arctan(x) have the form x + O(x³) and so
arctan( k tan(x) ) ≈ kx
should be a very good approximation for small x.
Here’s a plot of our function for varying values of k.
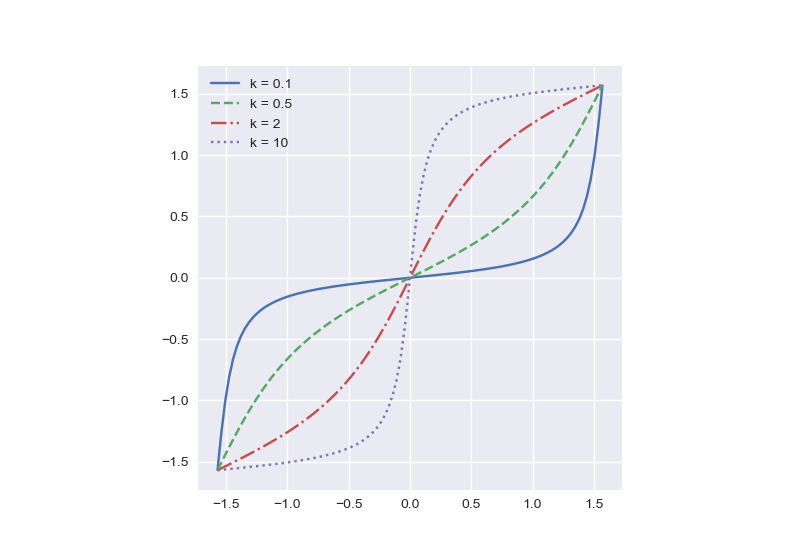
Each is fairly flat in the middle, with slope equal to its value of k.
As k increases, f(x; k) becomes more and more like a step function, equal to -π/2 for negative x and π/2 for positive x, i.e.
arctan( k tan(x) ) ≈ sgn(x) π/2
for large k. Here again we might have discussion like above.
- Novice: Set k = ±∞. Then ±∞ tan(x) = ±∞ and arctan(±∞) = ±π/2.
- Journeyman: You can’t do that!
- Expert: Well, you can if you interpret everything in terms of limits.

Hi John,
I discovered something interesting involving the tangent-constant commutator atan(k*tan(a)) form. It is this: one can represent an arbitrary rotated ellipse in polar coordinates r(a) using a formula that includes atan(k·tan(a)), where k is the ratio of the long and short axes of the un-rotated ellipse; further, one can represent the tangent angle of that ellipse (which is the derivative of r(a)) as atan(k²·tan(a)).
I have always found commutators interesting, ever since I learned about them in quantum mechanics. As you may know, another sort of commutator can be used in computer graphics to “zoom” to an arbitrary point in an image.