Sum of squared digits

Take a positive integer x, square each of its digits, and sum. Now do the same to the result, over and over. What happens?

To find out, let’s write a little Python code that sums the squares of the digits.

    def G(x):
        return sum(int(d)**2 for d in str(x))

This function turns a number into a string, and iterates over the characters in the string, turning each one back into an integer and squaring it.

Now let’s plot the trajectories of the iterations of G.

    def iter(x, n):
        for _ in range(n):
            x = G(x)
        return x
    for x in range(1, 40):
        y = [iter(x, n) for n in range(1, 12)]
        plt.plot(y)

This produces the following plot.

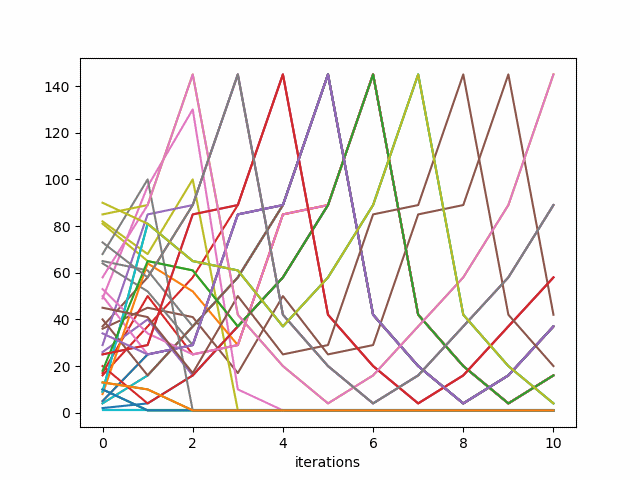
For every starting value, the sequence of iterations either gets stuck on 1 or it goes in the cycle 4, 16, 37, 58, 89, 145, 42, 20, 4, … . This is a theorem of A. Porges published in 1945 [1].

To see how the sequences eventually hit 1 or 4, let’s modify our iteration function to stop at 4 rather than cycling.

    def iter4(x, n):
        for _ in range(n):
            if x != 4:
                x = G(x)
        return x

    for x in range(1, 40):
        y = [iter4(x, n) for n in range(1, 16)]
        plt.plot(y)

This produces the following plot.

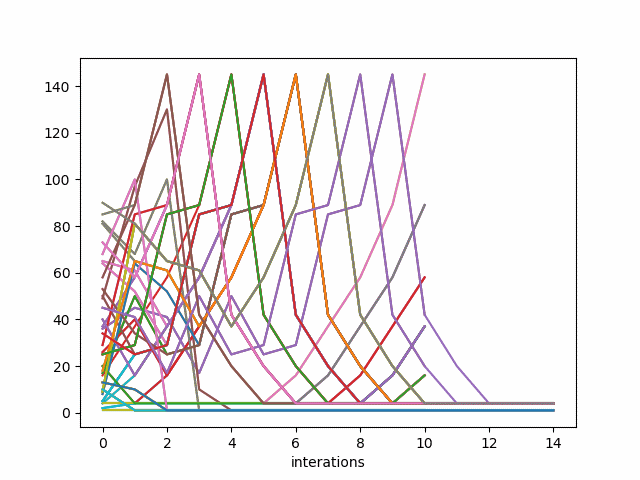
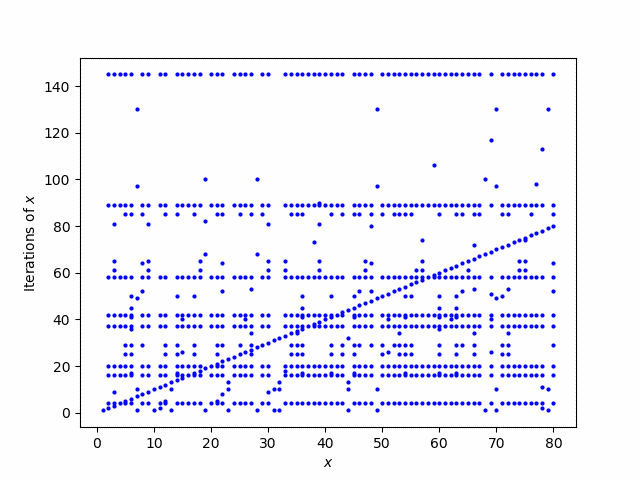
Update: Here’s a better, or at least complementary, way to look at the iterations. Now the horizontal axis represents the starting points x and the points stacked vertically over x are the iterates of G starting at x.

    def orbit(x):
        pts = set()
        while x not in pts:
            pts.add(x)
            x = G(x)
        return pts  

    for x in range(1, 81):
        for y in orbit(x):
            plt.plot(x, y, "bo", markersize=2)
    plt.xlabel("$x$")
    plt.ylabel("Iterations of $x$")
    plt.savefig("porges3.png")

[1] Porges, A set of eight numbers, Amer. Math. Monthly, 52(1945) 379-382.