Concentric circle images go wild

HAKMEM Item 123 gives two plots, both images of concentric circles under functions given by power series with rapidly thinning terms [1]. The first is the function

and the second is

The lower limits of summation are not given in the original. I assumed at first the sums began at n = 0, but my plots didn’t match the original until I set the lower index to begin at n = 1.

Here are the plots. First, the image of the circles of radius 1/2, 3/4, 7/8, and 1 under f.

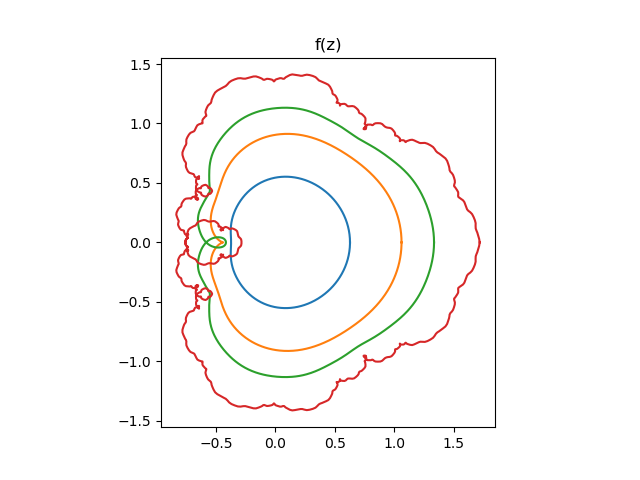
Next, the images of the circles of radius 1/8, 2/8, …, 8/8 under g.

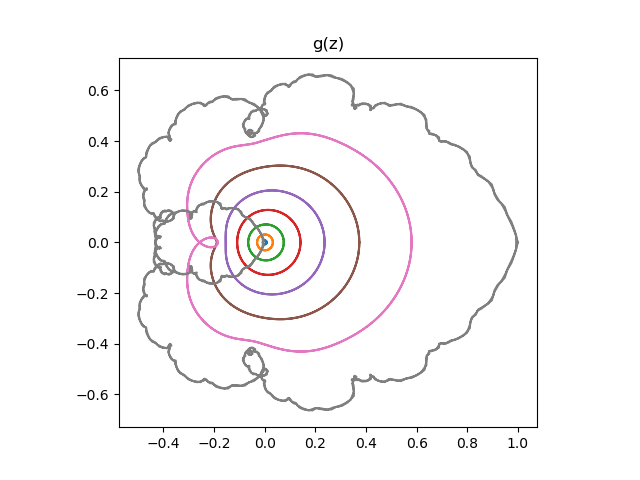
Note that the images of concentric circles are smooth, concentric, not self-intersecting for small radii. As the radii get larger, the images of the circles start to intersect. And when the radius is 1, the images are rough and reminiscent of Mandelbrot sets.

Here’s the Python code that produced the plots.

    from math import factorial
    from numpy import linspace, exp, pi
    import matplotlib.pyplot as plt
    
    def f(thin, z):
        return sum(z**thin(n)/thin(n)
                   for n in range(1, 12))
    
    theta = linspace(0, 2*pi, 1000)
    
    for r in [0.5, 0.75, 0.875, 1]:
        z = f(factorial, r*exp(1j*theta))
        plt.plot(z.real, z.imag)
    plt.axes().set_aspect(1)
    plt.title("f(z)")
    plt.show()
    plt.close()
    
    for n in range(8):
        r = (n+1)/8
        z = f(lambda n: 2**n, r*exp(1j*theta))
        plt.plot(z.real, z.imag)
    plt.title("g(z)")
    plt.axes().set_aspect(1)
    plt.show()

Update 1: Out of curiosity, I unrolled the plots to look at the real and imaginary components separately. Here’s what I got.

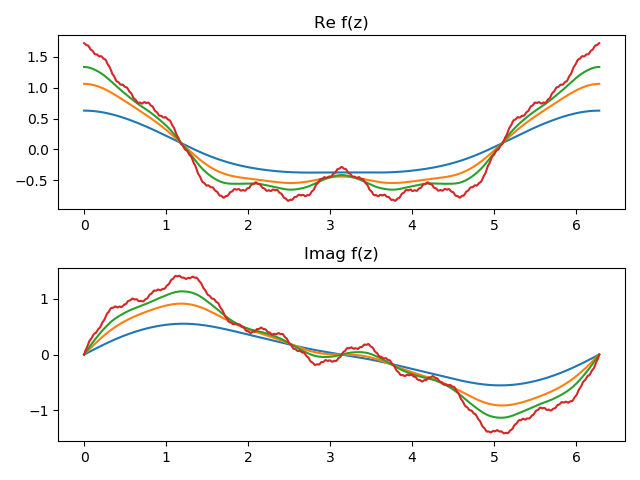
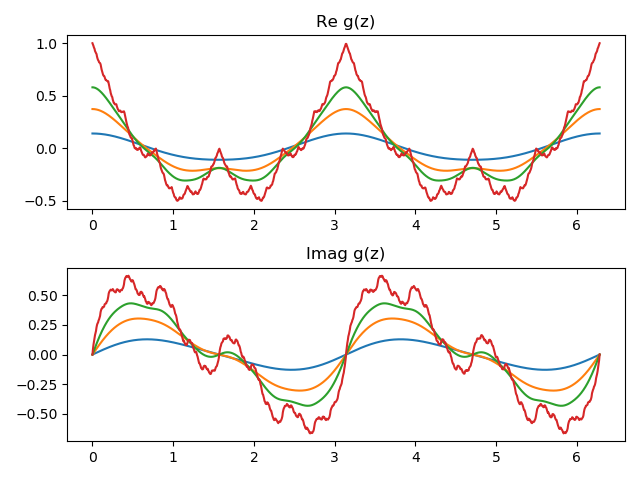
Update 2: Here’s a plot of the arclength of the image of a circle of radius r under the map g(z).

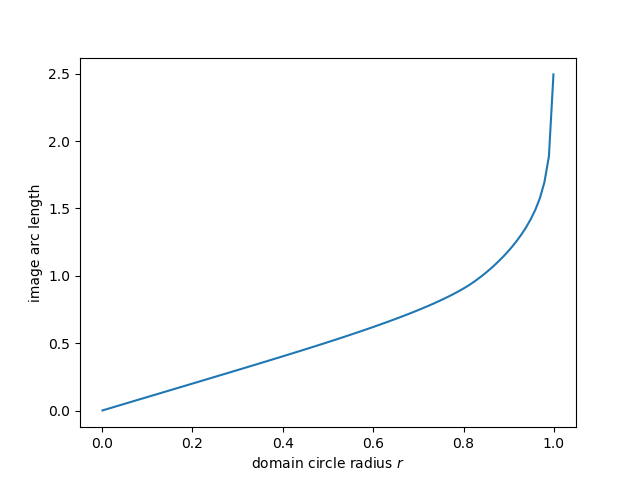
The length of the image curve is nearly proportional to the circumference of the input until r around 0.8, then the length increases quickly. Apparently the arc length goes to infinity as r goes to 1, though I haven’t proved this.

[1] See the footnote on lacunary series here.