Pythagorean dates

The numbers that make up today’s date—12, 16, and 20—form a Pythagorean triple. That is, 12² + 16² = 20².

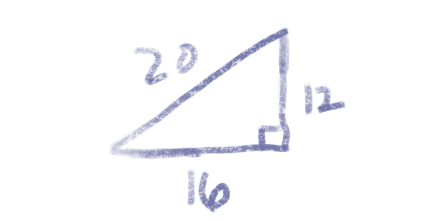
There won’t be any such dates next year. You could confirm this by brute force since there are only 365 days in 2021, but I hope to do something a little more interesting here.

The Mathematica function

    PowersRepresentations[n, k, p]

lists the ways to represent a number n as the sum of k pth powers. Calling PowersRepresentations[21^2, 2, 2] shows that there is no non-trivial way to write 21² as the sum of two powers; the only way is 0² + 21². You might try using the whole year rather than the last two digits, but there’s no non-trivial way to write 2021 as the sum of two powers either.

The paragraph above says that no Pythagorean triangle can have hypotenuse 21 or 2021. But could there be a Pythagorean date next year with 21 on one of the sides?

If the components of a date correspond to sides of a Pythagorean triangle, and one of the sides is 21, then the day must be on the hypotenuse because all the month numbers are less than 21, and that day must be greater than 21.

Let’s look for Pythagorean triangles with a side equal to 22, 23, …, 31 and see whether any of them have a 21 on the side.

The Mathematica command

    For[d = 22, d <= 31, d++, Print[PowersRepresentations[d*d, 2, 2]]]

returns

    {{0,22}}
    {{0,23}}
    {{0,24}}
    {{0,25},{7,24},{15,20}}
    {{0,26},{10,24}}
    {{0,27}}
    {{0,28}}
    {{0,29},{20,21}}
    {{0,30},{18,24}}
    {{0,31}}

This tells us that the only numbers from 22 to 31 that can be on the side of a Pythagorean triangle are 25, 26, 29, and 30.

The number 21 does appear in the list: (20, 21, 29) is a Pythagorean triple. But if the 29th of a month were a Pythagorean date next year, it would have to be the 20th month. Since we only have 12 months, there won’t be any Pythagorean dates next year.

The number 22, 23, and 24 can’t be written as sums of squares in a non-trivial way, so if there’s a Pythagorean date in the next few years it will have to be with the day of the month on the side. We can see from the output above that (7, 24, 25) is a Pythagorean triple, so the next Pythagorean date is 7/25/24, and the next after that is 7/24/25. And the next after that will be 10/24/26.

Incidentally, there is an algorithm for counting how many ways a number can be written as the sum of k squares, and it is implemented in Mathematica as Squares[k, n]. If you run SquaresR[2, 441] it will tell you that there are four ways to write 441 as the sum of two squares. But all four of these are trivial: (0, 21), (21, 0), (0, −21), and (−21, 0). Because every square can be written as the sum of two squares analogously, a return value of 4 means there are no non-trivial solutions.