The exponential sum page on this site draws lines between the consecutive partial sums of
where m is the month, d is the day, and y is the last two digits of the year.
The sum for today is unusually round:
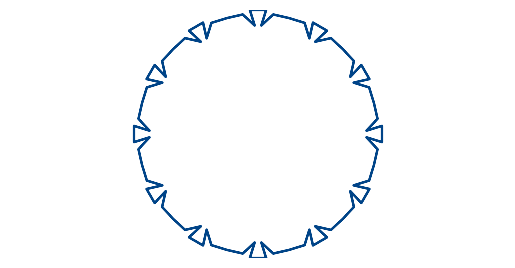
By contrast, the sum from yesterday is nowhere near round:
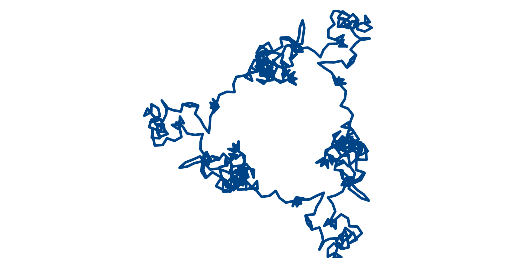
Out of curiosity, I looked at the numbers making up today’s sum. First, let’s look at the plot of today’s exponential sum with the axes.
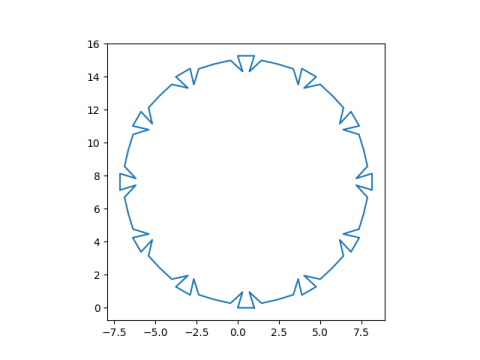
So the graph is not centered at the origin as you might implicitly expect. It does seem to be centered near zero on the real axis, but it’s centered somewhere near 8 on the imaginary axis.
If our graph is approximately a circle, its real and imaginary parts should be approximately sines and cosines. And that’s what we have.
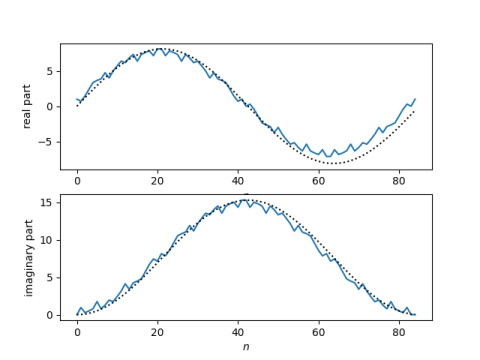
Going back to our original equation, we have empirically discovered that
Showing why the sum on the left should be roughly equal to the expression on the right is left as an exercise to the reader. :)

“So the graph is not centered at the origin as you might implicitly expect.”
Given that an empty sum is 0, I would expect the graph to pass through the origin, rather than being centered on it.
As for the exercise to the reader, a fairly simple explanation is that (n + 7)^3 is congruent to n^3 + 7 modulo 21 (since the intermediate terms vanish), so each sequence of 7 consecutive terms is the previous sequence of 7 terms rotated by 1/3 – 1/4 = 1/12 of a full circle. Given this, however, it seems like the real and imaginary parts should have the same amplitude.