What does the power tower mean and when does it converge?

This post will look at the “tower of powers”

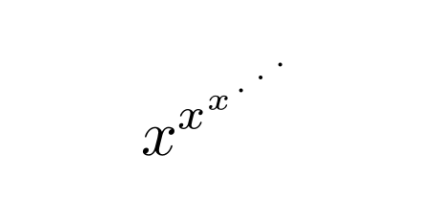
$x^{x^{x^{\iddots}}}$

and ask what it means, when it converges, and how to compute it. Along the way I’ll tie in two recent posts, including one that should come as a surprise.

First of all, the expression is right-associative. That is, it is the limit of

x^(x^(x^…))

and not the limit of

((x^x)^x)^…)

This means we evaluate our tower from the top down, which is a little strange to think about. But if we interpreted our tower as left-associative, building the tower from the bottom up, the sequence would be much less interesting: the limit would be 1 for 0 < x ≤ 1, and infinity for x > 1.

A few weeks ago I wrote about the special case of x equal to the imaginary unit. I looked at the sequence

$i, i^i, i^{i^i}, \ldots$

and the pattern the it makes in the complex plane.

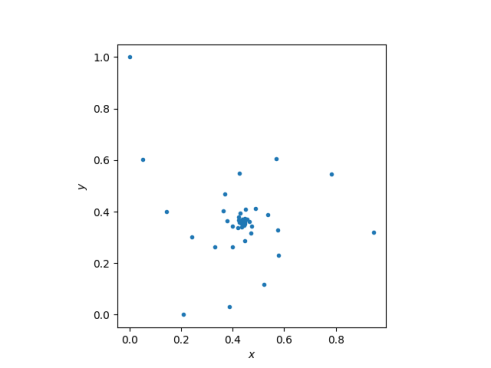
We can see that the iterates converge to somewhere around 0.4 + 0.4i.

This post will replace i with a real number x. Leonard Euler discovered a long time ago that the “tower of power” converges for x between e^–e and e^1/e. See[1].

Furthermore, for those x‘s where the sequence converges, it converges to an expression involving the Lambert W function which I wrote about in my previous post.

The power tower can be written in Donald Knuth’s up arrow notation as the limit of

$x \uparrow \uparrow n$

as n goes to infinity. The equation relating this limit to Lambert’s W function is

$\lim_{n\to\infty}x\uparrow \uparrow n = - \frac{W(-\log x)}{\log x}$

Let’s try this out numerically. Euler tells us the limit exists for x in the interval [e^–e , e^1/e] which is roughly [0.07, 1.44].

We’ll do this at the Python REPL. First we import functions to compute log and W.

    >>> from math import log
    >>> from scipy.special import lambertw as w

Now if we have correctly found our limit y, then x^y should equal y. The following shows that this is the case.

    >>> x = 0.07
    >>> y = -w(-log(x))/log(x)
    >>> y
    0.37192832251839264
    >>> x**y
    0.37192832251839264

    >>> x = 1.44
    >>> y = -w(-log(x))/log(x)
    >>> y
    2.3938117482029475
    >>> x**y
    2.393811748202947

By the way, we’ve said which real values of x cause the series to converge. But my first post on iterated powers looked at x = i. For which complex values does the series converge? I suspect the domain is a complicated fractal, but I don’t know that for sure.

[1] Brian Hayes. Why W? American Scientist. Vol 93, pp 104–109.

Tower of powers and convergence

Related posts

One thought on “Tower of powers and convergence”