A while back I wrote about a simple equation for the shape of an egg. That equation is useful for producing egg-like images, but it’s not based on extensive research into actual eggs.
I recently ran across a more realistic, but also more complicated, equation for modeling the shape of real eggs [1]. The equation models the shape of an egg by rotating the graph of a function of the form
y = (B/2) f(x; L, w, D)
around the x-axis. The parameters B and L are simple to describe, but w and D take a little more explanation.
Parameters
Imagine the egg positioned so the x-axis runs along the center of the egg, with the fat end on the left at −L/2 and the pointy end on the right at L/2. So L is the length of the egg.
The parameter B is the maximum breadth of the egg, the maximum diameter perpendicular to the central axis. If you plot y above as a function of x, the maximum value of y is B/2.
The authors describe w as “the parameter that shows the distance between two vertical axes corresponding to the maximum breadth and the half length of the egg.” I find that description confusing. I believe they’re saying that −w is the location of the maximum of y. So B/2 is the maximum value of y, and –w is where that maximum occurs.
The authors define a parameter DL/4 that I’m calling D for simplicity. They define this parameter as the “egg diameter at the point of L/4 from the pointed end.” That is, D is twice the value of y at x = L/4. Recall that the egg runs from −L/2 to L/2, so we’re talking about the point 3/4 of the way between the fat end and the pointed end.
To summarize, L, B, w, and D are the length, maximum breadth, the negative of the location of the maximum breadth, and the breadth three quarters of the way between the fat and pointed ends.
Equation
With all that out of the way, here’s the equation. I’ll write it up in Python, but I wanted to include a screen shot from the paper in case I made an error in coding it up.
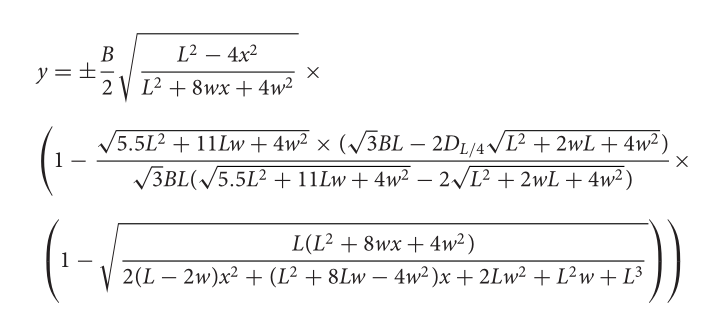
Python implementation
Here’s Python code that implements this function, if I haven’t made any errors.
from numpy import sqrt
def egg_radius(x, L, B, w, D):
# Note that k does not involve x
k = sqrt(5.5*L**2 + 11*L*w + 4*w**2)
k *= sqrt(3)*B*L - 2*D*sqrt(L**2 + 2*w*L + 4*w**2)
k /= sqrt(3)*B*L
k /= sqrt(5.5*L**2 + 11*L*w + 4*w*w) - 2*sqrt(L**2 + 2*w*L + 4*w**2)
# coefficients of a quadratic in x
a = 2*(L-2*w)
b = L**2 + 8*L*w - 4*w**2
c = 2*L*w**2 + L**2*w + L**3
t = L*(L**2 + 8*w*x + 4*w**2)
t /= a*x**2 + b*x + c
y = 0.5*B*sqrt(L**2 - 4*x**2)/sqrt(L**2 + 8*w*x + 4*w**2)
y *= (1 - k*(1 - sqrt(t)))
return y
Here’s a plot using this code:
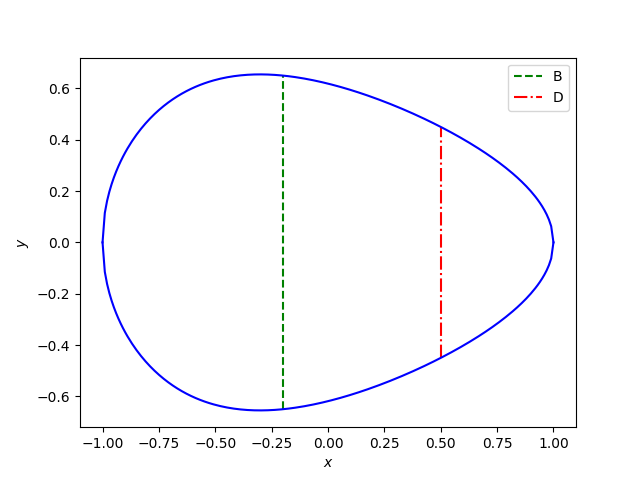
And here’s the code that was used to make the plot:
from numpy import linspace
import matplotlib.pyplot as plt
L = 2
B = 1.3
w = 0.2
D = 0.9
plt.plot([-w, -w], [-B/2, B/2], 'g--')
z = egg_radius(L/4, L, B, w, D)
plt.plot([L/4, L/4], [-z, z], "r-.")
x = linspace(-L/2, L/2, 200)
y = egg_radius(x, L, B, w, D)
plt.plot(x, y, 'b')
plt.plot(x, -y, 'b')
plt.legend(["B", "D"])
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.show()
Error
Something does add up. It appears that y(−w) = B, as it should, but the maximum of y is not at −w.
from scipy.optimize import minimize_scalar
print(-w, egg_radius(-w, L, B, w, D))
res = minimize_scalar(lambda x: -egg_radius(x, L, B, w, D), bracket=[-1,0,1], method='brent')
print(res.x, egg_radius(res.x, L, B, w, D))
This shows the maximum is near −0.3, not at −0.2.
Maybe I’ve misunderstood something or made a coding error. Or maybe there’s an error in the paper.
Maybe the breadth you specify is a target and not something that is always exactly achieved?
***
[1] Egg and math: introducing a universal formula for egg shape. Valeriy G. Narushin, Michael N. Romanov, Darren K. Griffin. Annals of the New York Academy of Sciences. Published online August 23, 2021.

I can’t help with the question about w, but I will suggest that when you’re plotting physical measurements, it’s good to force the x and y axes to have the same scale (even though yours aren’t too far off). Add these lines:
ax = plt.gca()
ax.set_aspect(‘equal’)
The sad truth is that the paper is wrong as x=-w is only the maximum for the original, unmodified, formula but not for the one they found.
You are right about y(-w) and B not always equal
but i think this is a limitation in the formula