When derivative equals inverse

Is there a function whose derivative is its inverse? In other words, is there a function f that satisfies

f ‘(x) = f^-1(x)

for positive x? Indeed there is one given here.

Let φ be the golden ratio (√5 + 1)/2. Then for x > 0 the function

f(x) = φ (x/φ)^φ

satisfies our equation. It’s derivative is its inverse. To prove this, calculate

f ‘( f(x) )

and find that it equals x. The reason the golden ratio comes up is that if

f(x) = k (x/k)^k

is a solution then k must satisfy

k² – k = 1

and φ is a solution.

Whenever you see one root of a quadratic equation, it’s natural to wonder about the other root. In this case

ψ = -1/φ

is the other root to our quadratic equation.  Could we have used ψ rather than φ? Yes, but the solution would blow up at 0. By using φ, our solution can be extended to allow not just x > 0 but x ≥ 0.

We could also define f for x < 0 using k = φ or k = ψ. But the former blows up as x approaches 0 from the left and the latter does not. So if we use k = ψ to the left of 0 and k = φ to the right, we get a function defined for all real x. That is, we can define

f(x) = φ (x/φ)^φ   for x ≥ 0

f(x) = ψ (x/ψ)^ψ   for x < 0

and have a continuous function on the whole real line.

We need to be a little careful here about what we mean by raising a negative number to an irrational exponent. To be more explicit we should say

f(x) = φ (x/φ)^φ   for x ≥ 0

f(x) = -ψ (-x/ψ)^ψ   for x < 0

Here’s a plot:

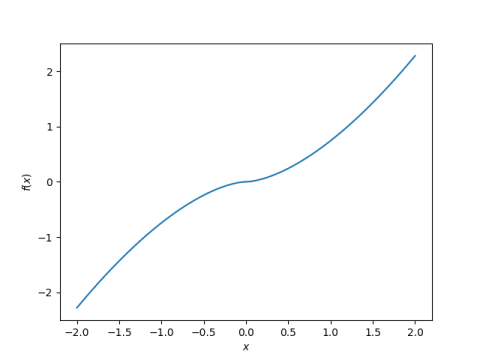
Just to quickly open up a new can of worms before I close this out, you could go back to the definition

f(x) = φ (x/φ)^φ

for x > 0 and consider it a function of a complex variable. You could extend it to most of the complex plane, but you’d have to have a branch cut that includes the origin. The construction above wouldn’t work because the function is not analytic at 0. In fact, it’s not twice differentiable at 0.