Will Buckner sent me an email with the following question recently. (I’m sharing this with permission.)
I am building a kiln using a catenary arch. The rear wall and front wall/door will be vertical and fill in the space under the arch, which has the dimensions of 41″W x 39.5″H. I need the area within this arch in order to calculate how many bricks I need to construct the two walls. Can you help me calculate that area?
Here’s my solution. I fit a parabola and a catenary in part to check my work and in part to see how different they are.
Parabola
We’ll start with a parabola as our warmup because it’s easier.
Let w = 41 and h = 39.5. We want a quadratic function y(x) such that y(0) = h and y(±w/2) = 0.
Assume y has the form
y(x) = b − ax²
y(0) = h leads to the conclusion that b = h, and y(±w/2) = 0. leads to
a(w/2) = h
And this leads to the final form.
y = h(1 – (2x/w)²)
Catenary
Our catenary will have the form
y(x) = b – a cosh(x/a)
and again y(0) = h and y(±w/2) = 0. These two requirements lead to the equations
b − a = h
and
b − a cosh(w/2a) = 0.
Then
b = h + a
and
h + a (1 − cosh(w/2a) = 0.
The latter equation cannot be solved in closed form, but it’s easy enough to solve numerically. When I asked Mathematica to compute the root with
FindRoot[39.5 + a - a Cosh[20.5/a] == 0, a]
it failed. Then I plotted the function, saw that the root was around 8.5, then gave Mathematica a hint.
FindRoot[39.5 + a - a Cosh[20.5/a] == 0, {a, 8.5}]
Then Mathematica came back with
a = 8.475359432102444.
So the equation of our catenary is
y = h + a(1 – cosh(0.5 x/a))
where h and a are given above.
Plots
Here’s a plot of both curves. The blue curve inside is the parabola, and the gold curve on the outside is the catenary.
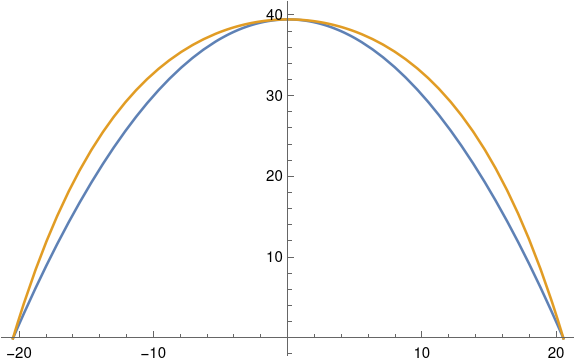
Here’s the code that made the plot.
Plot[{h (1 - (2 x/w)^2), h + a - a Cosh[x/a] }, {x, -w/2, w/2}]
Area
And now for the area, the thing I was asked to find. For the parabola
Integrate[h (1 - (2 x/w)^2), {x, -w/2, w/2}]
returns 1079.67. For the catenary,
Integrate[h + a (1 - Cosh[x/a]), {x, -w/2, w/2}]
returns 1166.56.
The number of bricks this will take is roughly the area of the arch divided by the area of a brick, but being more precise is a complicated question that depends on how much mortar you use, and how you use plan to use rectangular bricks to make a curved arch.
