Sinc approximation to Bessel function

The Bessel functions J_n for even n look something like the sinc function. How well can you approximate the former by sums of the latter? To make things concrete, we’ll approximate J₂. Here’s a plot of J₂.

J_2

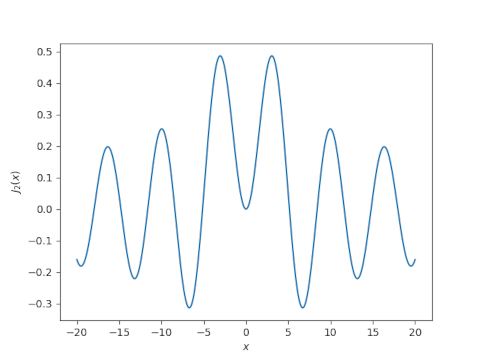
And here’s a plot of sinc(x) = sin(πx)/πx.

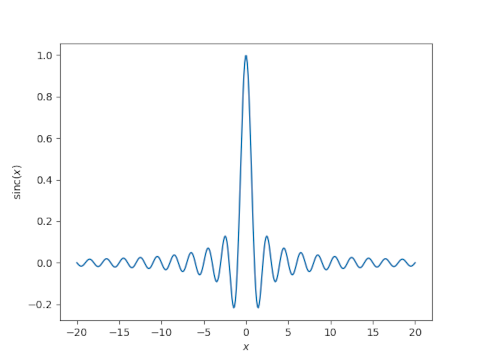
sinc(x)

The sinc approximation for a function f(x) is given by

$f(x) \approx \sum_{j=-n}^n f(jh) \, \text{sinc}\left(\frac{x - jh}{h}\right)$

Sinc approximation can be remarkably accurate, nearly optimal in some sense.

The accuracy of the approximation increases as n gets larger and h gets smaller. We will fix n = 10. How should we pick h? The paper cited in this post suggests using

$h = \frac{\pi}{2} \sqrt{\frac{1}{2n}} = 0.35124$

Let’s try that and see what happens.

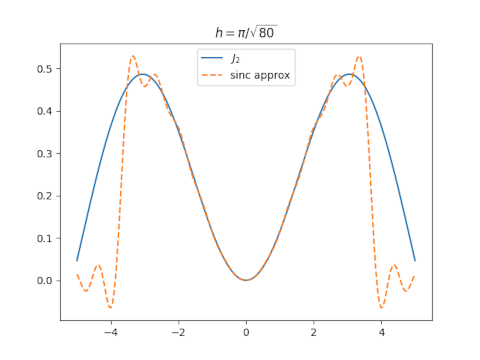
The approximation isn’t very good overall, though it’s excellent near 0.

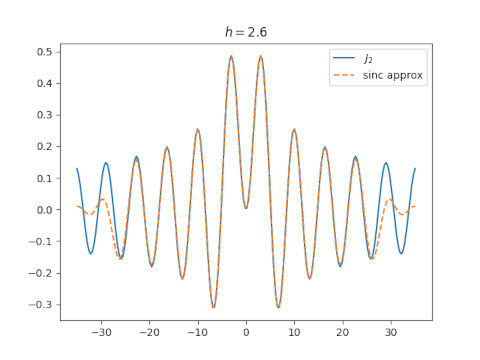
Before making plots, I had a plausible argument for why the value of h suggested above might be optimal. I also had an argument for why a much larger value of h, something on the order of 8 might be optimal. Turns out both are wrong. You can get a good approximation over a larger range by choosing h around 2.6.

Related posts