This post will explore how the trigonometric functions and the hyperbolic trigonometric functions relate to the Jacobi elliptic functions.
There are six circular functions: sin, cos, tan, sec, csc, and cot.
There are six hyperbolic functions: just stick an ‘h’ on the end of each of the circular functions.
There are an infinite number of elliptic functions, but we will focus on 12 elliptic functions, the Jacobi functions.
sn, sin, and tanh
The Jacobi functions have names like sn and cn that imply a relation to sine and cosine. This is both true and misleading.
Jacobi functions are functions of two variables, but we think of the second variable as a fixed parameter. So the function sn(z, m), for example, is a family of functions of z, with a parameter m. When that parameter is set to 0, sn coincides with sine, i.e.
sn(z, 0) = sin(z).
And for small values of m, sn(z, m) is a lot like sin(z). But when m = 1,
sn(z, 1) = tanh(z).
Think of m as a knob attached to the sn function. When we turn the knob to 0 we get the sine function. As we turn the knob up, sn becomes less like sine and more like hyperbolic tangent. The period becomes longer as a function of m, diverging to infinity as m approaches 1. Here’s a plot of one period of sn(x, m) for several values of m.
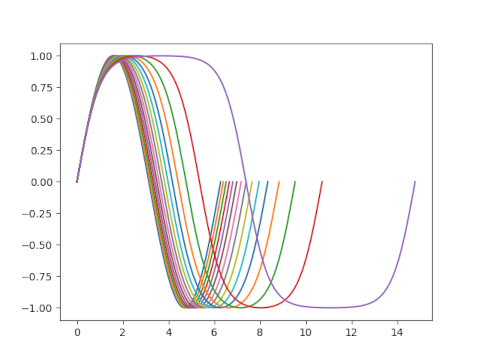
So while it’s true that sn can be thought of as a generalization of sine, it’s also a generalization of hyperbolic tangent.
Similarly, cn can be thought of as a generalization of cosine, but it’s also a generalization of hyperbolic secant.
All of the Jacobi functions are circular functions when m = 0 and hyperbolic functions when m = 1, with a caveat that we’ll get to shortly.
The extra function
For the rest of this article, I’d like to say there are seven circular functions, making the constant function 1 an honorary trig function. I’d also like to call it a hyperbolic function and a Jacobi function.
With this addition, we can say that the seven circular functions consist of {sin, cos, 1} and all their ratios. And the seven hyperbolic functions consist of {sinh, cosh, 1} and all their ratios.
The 13 Jacobi functions consist of {sn, cn, dn, 1} and all their ratios.
Circular functions are Jacobi functions
I mentioned above that sn(z, 0) = sin(z) and cn(z, 0) = cos(z). And the honorary Jacobi function 1 is always 1, regardless of m. So by taking ratios of sn, cn, and 1 we can obtain all ratios of sin, cos, and 1. Thus all circular functions correspond to a Jacobi function with m = 0.
There are more Jacobi functions than circular functions. We’ve shown that some Jacobi functions are circular functions when m = 0. Next we’ll show that all Jacobi functions are circular functions when m = 0. For this we need one more fact:
dn(z. 0) = 1.
Never mind what dn is. For the purpose of this article it’s just one of the generators for the Jacobi functions. Since all the generators of the Jacobi functions are circular functions when m = 0, it follows that all Jacobi functions are circular functions when m = 0. Note that this would not be true if we hadn’t decided to call 1 a Jacobi function.
Hyperbolic functions are Jacobi functions
We can repeat the basic argument above to show that when m = 1, hyperbolic functions are Jacobi functions and Jacobi functions are hyperbolic functions.
I mentioned above that sn(z, 1) = tanh(z) and cn(z, 1) = sech(z). I said above that the hyperbolic functions are generated by {sinh, cosh, 1} but they are also generated by {tanh, sech, 1} because
cosh(z) = 1/sech(z)
and
sinh(z) = tanh(z) / sech(z).
A set of generators for the hyperbolic functions are Jacobi functions with m = 1, so all hyperbolic functions and Jacobi functions with m = 1. To prove the converse we also need the fact that
dn(z, 1) = sech(z).
Since sn, cn, dn, 1 correspond to hyperbolic functions when m = 1, all Jacobi functions do as well.
When Jacobi functions aren’t elliptic
The Jacobi functions are elliptic functions in general, but not when m = 0 or 1. So it’s not quite right to say that the circular and hyperbolic functions are special cases of the Jacobi elliptic functions. More precisely, they are special cases of the Jacobi functions, functions which are almost always elliptic, though not in the special cases discussed here. You might say that circular and hyperbolic functions are degenerate elliptic functions.
Elliptic functions are doubly periodic. They repeat themselves in two independent directions in the complex plane.
Circular functions are periodic along the real axis but not along the imaginary axis.
Hyperbolic functions are periodic along the imaginary axis but not along the real axis.
Jacobi functions have a horizontal period and a vertical period, and both are functions of m. When 0 < m < 1 both periods are finite. When m = 0 the vertical period becomes infinite, and when m = 1 the horizontal period becomes infinite.
