Square root factorial

What factorial is closest to the square root of 2024 factorial?

A good guess would be 1012, based on the idea that √(n!) might be near (n/2)!.

This isn’t correct—the actual answer is 1112—but it’s not wildly off.

Could it be that (2n)! is asymptotically (n!)²?

No, Gauss’ duplication formula

$\Gamma(2z) = \frac{1}{\sqrt{2\pi}} 2^{2z - 1/2} \Gamma(z) \Gamma\left(z + \frac{1}{2}\right)$

shows that the ratio of (2n)! to (n!)² grows exponentially as a function of n.

However, the ratio only grows exponentially, and factorials grow faster than exponentially. I believe that the value of m minimizing

| √(n!) – m! |

asymptotically approaches n/2. In other words, the inverse factorial of √(n!) approaches n/2. And more generally the inverse factorial of (n!)^1/k asymptotically approaches n/k. I haven’t written out a proof, but the plot below shows numerical evidence.

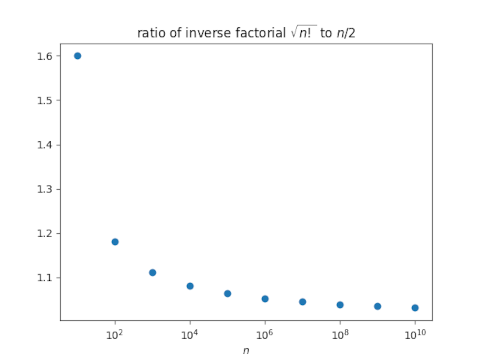
So √(n!) is not asymptotically (n/2)!, but the inverse factorial of √(n!) is asymptotically n/2.

See the next post for a way to compute inverse factorials.

One thought on “Square root factorial”

Konstantinos Panagiotou

2 January 2024 at 11:29

You are right! By Stirling‘s formula, as m,n get large,

m! ~ (m/e)^m sqrt(2 Pi m)

and

sqrt(n!) ~ (n/e)^(n/2) (2 Pi n)^(1/4)

where ~ means 1+o(1). By equating the right hand sides we obtain that

m = n/2 + O(n/log(n))

and we can actually derive an asymptotic expansion for m.

Comments are closed.