Probability of rolling a Yahtzee

Posted on 19 May 2025 by John

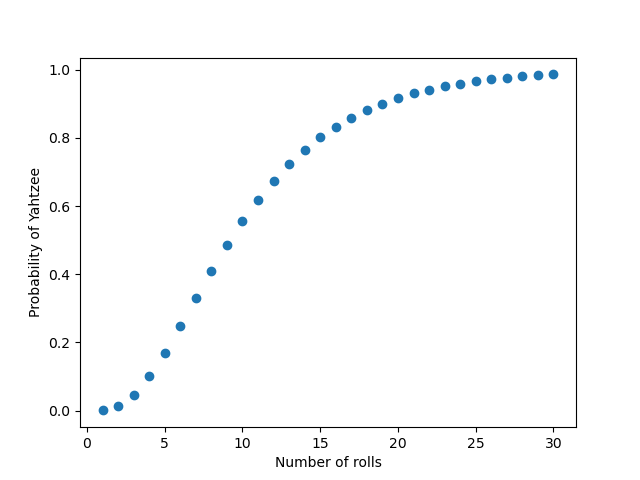
IJK (@iconjack) has calculated the probability of rolling a Yahtzee in no more than n rolls.

$\begin{align*} p(n) &= 1 + \frac{53}{13}\left(\frac{5}{6}\right)^{2n+1} + \frac{11\cdot 5^n}{13\cdot 2^{n+5}\cdot3^{3n+1}} \\ &\phantom{=} - \frac{5^n}{8\cdot 3^{2n-2}} - \frac{7\cdot 5^{n+1}}{2^{n+5}\cdot 3^{n-1}} \end{align*}$

The first few numerical values are:

p(1) = 0.0007716
p(2) = 0.0126316
p(3) = 0.0460286

The probability is 0.95 after 23 rolls, and 0.99 after 32 rolls.

Here’s a plot.

Leave a Reply