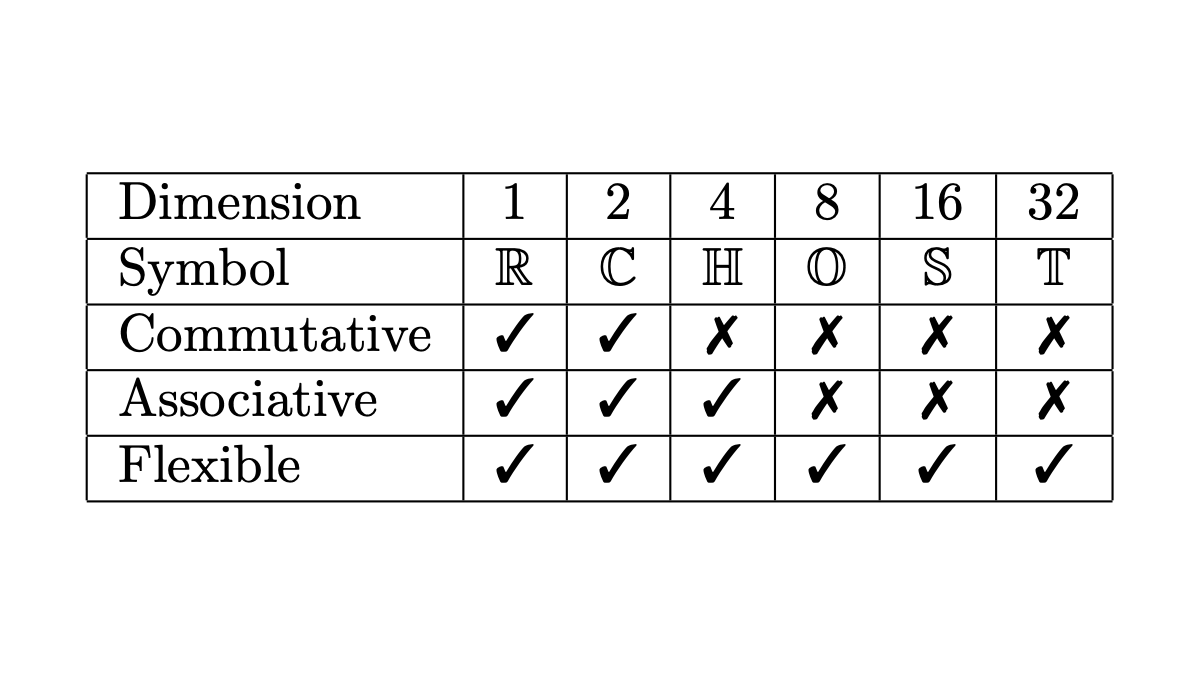
You can multiply pairs of real numbers using the rules of complex numbers. Complex numbers have all the algebraic structure of the real numbers, i.e. they form a field.
There is a general process, the Cayley-Dickson construction, that let’s you bootstrap multiplication from 1 real number to 2, from 2 to 4, from 4 to 8, etc. You can repeat the process as many times as you like, defining multiplication on lists of 2n numbers, but you lose structure as you go.
Quaternions
Multiplication for 4-tuples gives the quaternions. The quaternions retain most of the structure of the real and complex numbers. Multiplication is associative. Non-zero elements have a multiplicative inverse, i.e. you can divide. And multiplication plays well with the norm:
|| xy || = || x || · || y ||.
But multiplication is not commutative: in general, xy ≠ yx,
Octonions
Multiplication of 8-tuples produces the octonions . It’s still true that non-zero elements have a multiplicative inverse, and multiplication still plays well with the norm as above. But now, not only is multiplication not commutative, it’s not even associative: in general, (xy)z ≠ x(yz). It’s the “in general” part that this post wants to elaborate on.
The subalgebra generated by any two elements is associative. That means, for example, that (xy)x = x(yx). If you fix x and y, and look at all the octonions you can form by taking adding, multiplying, conjugating, and inverting these elements, as well as multiplying them by a real number, you get a set of octonions for which multiplication is associative.
In fact, the subalgebra generated by two octonions is isomorphic to either the real numbers, the complex numbers, or the quaternions, depending on the two octionions you start with.
This was brought to my attention by a common on a post on octonions from a few years ago. Someone pointed out that an equation I had written
x* = − (x + (e1 x) e1 + … + (e7 x) e7) / 6
could be written more simply as
x* = − (x + e1 x e1 + … + e7 x e7) / 6.
because each term only involves two distinct octonions.
Sedenions
The next step, multiplying 16-tuples of real numbers, gives the sedenions [1]. Now we lose even more structure. Multiplication is not commutative, not associative, and it’s possible for two non-zero numbers to have a zero product. That means the norm property
|| xy || = || x || · || y ||
goes out the window since the left size can be zero when the right side is not.
Also, sedenions do not have the weak associative property (xy)x = x(yx) that octonions do.
Trigintaduonions
The next rung in the Cayley-Dickson ladder is the family of 32-tuples known as the trigintaduonions [2]. The sedenions are a mess, and they’re a subset of the trigintaduonions, so the trigintaduonions are a mess.
More octonion posts
- Error correcting code based on octonions
- Python code for multiplying octionions and friends
- How close are octonions to being associative?
[1] From the Latin word sedecim for 16.
[2] From the Latin triginta for 30 and duo for 2.