The sinc function
sinc(x) = sin(x) / x
comes up continually in signal processing. If x is moderately small, the approximation
sinc(x) ≈ (2 + cos(x))/3
is remarkably good, with an error on the order of x4/180. This could be useful in situations where you’re working with the sinc function and the x in the denominator is awkward to deal with and you’d rather have a pure trig function.
Here’s a plot:
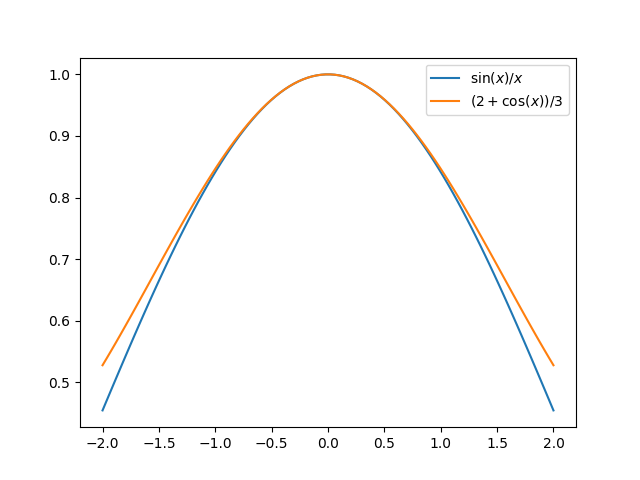
Of course the approximation is only good for small x. For large x the sinc function approaches zero while (2 + cos(x))/3 oscillates with constant amplitude forever.
When the approximation is good, it is very, very good, which reminds me of this nursery rhyme.
There was a little girl,
Who had a little curl,
Right in the middle of her forehead.
When she was good,
She was very, very good,
But when she was bad, she was horrid.
