For a positive real number x, the expression x mod 1 means the fractional part of x:
x mod 1 = x − ⌊ x ⌋.
This post will look at the distributions of nx mod 1 and xn mod 1 for n = 1, 2, 3, ….
The distribution of nx mod 1 is easy to classify. If x is rational then nx will cycle through a finite number of values in the interval [0, 1]. If x is irrational then nx will be uniformly distributed in the interval.
The distribution of xn mod 1 is more subtle. We have three basic facts.
- If 0 ≤ x < 1, then xn → 0 as n → ∞.
- If x = 1 then xn = 1 for all n.
- For almost all x > 1 the sequence xn mod 1 is uniformly distributed. But for some values of x it is not, and there’s no known classification for these exceptional values of x.
The rest of the post will focus on the third fact.
Suppose x = √2. Then for all even n, xn mod 1 = 0. The sequence isn’t uniformly distributed in [0, 1] because half the sequence is piled up at 0.
For another example, let’s look at powers of the golden ratio φ = (1 + √5)/2. For even values of n the sequence φn converges to 1, and for odd values of n it converges to 0. You can find a proof here.
At one time it was not known whether xn mod 1 is uniformly distributed for x = 3 + √2. (See HAKMEM, item 32.) I don’t know whether this is still unknown. Let’s see what we can tell from a plot.
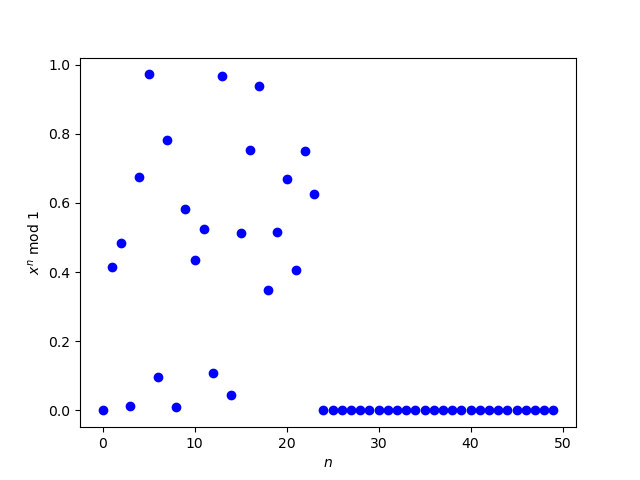
Apparently sometime around n = 25 the sequence suddenly converges to 0. That looks awfully suspicious. Let’s calculate x25 using bc.
$ echo '(3 + sqrt(2))^25' | bc -l
13223107213151867.43024035874391918714
This says x25 mod 1 should be around 0.43, not near 0. The reason we’re seeing all zeros is that all the bits in the significand are being used to store the integer part and none are left over for the fractional part. A standard floating point number has 53 bits of significand and
(3 + √2)25 > 253.
For more details, see Anatomy of a floating point number.
Now let’s see what happens when we calculate xn mod 1 correctly using bc. Here’s the revised plot.
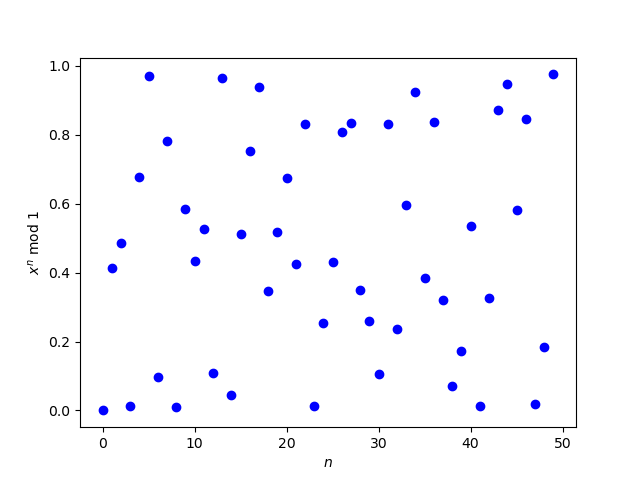
Is this uniformly distributed? Well, it’s not obviously not uniformly distributed. But we can’t tell by looking at a plot because uniform distribution is an asymptotic property.
We didn’t give the definition of a uniformly distributed sequence until now because an intuitive understanding of the term was sufficient. Now we should be more precise.
Given a set E, a sequence ω, and an integer N, define A(E, ω, N) to be the number of elements in the first N elements of the sequence ω that fall inside E. We say ω is uniformly distributed mod 1 if for every 0 ≤ a ≤ b ≤ 1,
limN → ∞ A([a, b), ω, N) / N = b − a.
That is, the relative port of points that fall in an interval is equal to the length of the interval.
Now let’s go back to the example x = √2. We know that the powers of this value of x are not uniformly distributed mod 1. But we also said that for almost all x > 1 the powers of x are uniformly distributed. That means every tiny little interval around √2 contains a number y such that the powers of y are uniformly distributed mod 1. Now if y is very close to √2 and we plot the first few values of yn mod 1 then half of the values will be near 0. The sequence will not look uniformly distributed, though it is uniformly distributed in the limit.
