Yesterday’s post looked at the distribution of powers of x mod 1. For almost all x > 1 the distribution is uniform in the limit. But there are exceptions, and the post raised the question of whether 3 + √2 is an exception.
A plot made it look like 3 + √2 is an exception, but that turned out to be a numerical problem.
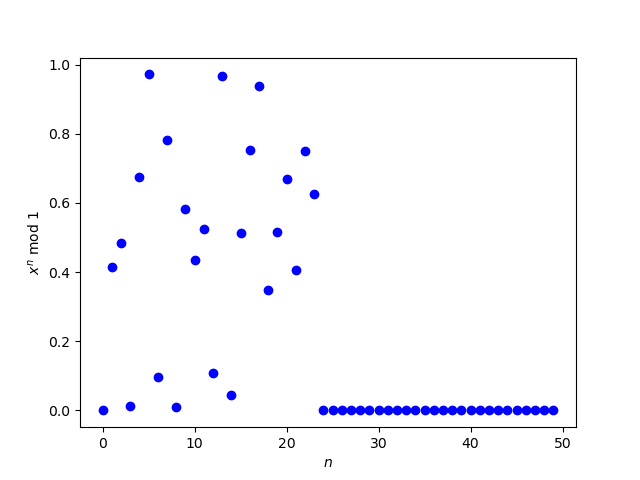
A higher precision calculation showed that the zeros on the right end of the plot were erroneous.
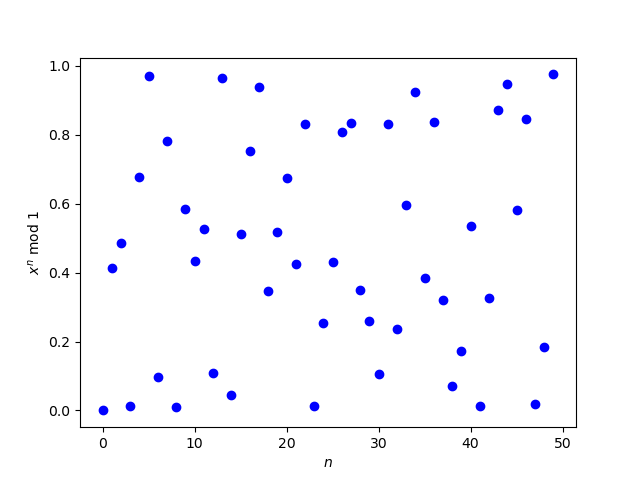
So this raises the question of how to calculate (3 + √2)n accurately for large n. The way I created the second plot was to use bc to numerically calculate the powers of 3 + √2. In this post, I’ll look at using Mathematica to calculate the powers symbolically.
For all positive integers n,
(3 + √2)n = an + bn√2
where an and bn are positive integers. We want to compute the a and b values.
If you ask Mathematica to compute (3 + √2)n it will simply echo the expression. But if you use the Expand function it will give you want. For example
Expand[(3 + Sqrt[2])^10]
returns
1404491 + 993054 √2
We can use the Coefficient function to split a + b √2 into a and b.
parts[n_] :=
Module[{x = (3 + Sqrt[2])^n},
{Coefficient[x, Sqrt[2], 0], Coefficient[x, Sqrt[2], 1]}]
Now parts[10] returns the pair {1404491, 993054}.
Here’s something interesting. If we set
(3 + √2)n = an + bn√2
as above, then the two halves of the expression on the right are asymptotically equal. That is, as n goes to infinity, the ratio
an / bn√2
converges to 1.
We can see this by defining
ratio[n_] :=
Module[ {a = Part[ parts[n], 1], b = Part[parts[n], 2]},
N[a / (b Sqrt[2])]]
and evaluating ratio at increasing values of n. ratio[12] returns 1.00001 and ratio[13] returns 1, not that the ratio is exactly 1, but it is as close to 1 as a floating point number can represent.
This seems to be true more generally, as we can investigate with the following function.
ratio2[p_, q_, r_, n_] :=
Module[{x = (p + q Sqrt[r])^n},
N[Coefficient[x, Sqrt[r], 0]/(Coefficient[x, Sqrt[r], 1] Sqrt[r])]]
When r is a prime and
(p + q√r)n = an + bn√r
then it seems that the ratio an / bn √r converges to 1 as n goes to infinity. For example, ratio2[3, 5, 11, 40] returns 1, meaning that the two halves of the expression for (3 + 5√11)n are asymptotically equal.
I don’t know whether the suggested result is true, or how to prove it if it is true. Feels like a result from algebraic number theory, which is not something I know much about.
Update: An anonymous person on X suggested a clever and simple proof. Observe that
In this form it’s clear that the ratio an / bn √2 converges to 1, and the proof can be generalized to cover more.

You shouldn’t need algebraic number theory just some basic linear algebra. The formula for $a_n$ and $b_n$ expresses them as a vector times a power of a matrix. So they converge directionally onto the eigenvector with the biggest eigenvalue and it happens that eigenvector has the ratio one. Of course have to write this all down and check it works.
That sounds promising!
Your final observation about the ratio is correct (and doesn’t depend on r being prime; it only requires that it not be a square).
If (p + q sqrt r)^n = an + bn sqrt r, with p,q,an,bn rational, then (p – q sqrt r) = an – bn sqrt r (same an, bn) as you can easily see e.g. by expanding the brackets or by observing that sqrt r and – sqrt r are both equally good square roots of r.
So write u = p + q sqrt r, v = p – sqrt r. Then an = (u^n+v^n)/2 and bn sqrt r = (u^n-v^n)/2, and the ratio is (u^n+v^n)/(u^n-v^n). If we write w = v/u then this equals (1+w^n)/(1-w^n).
If p,q are positive then |w| 1.
Maybe this can be studied more analytically? If $x=a_1+b_1\sqrt{2}$, and we write $x^n = a_n + b_n\sqrt{2}$, then we can make a $2×2$ matrix $M$ so that $M^n (1, 0) = (a_n, b_n)$. Maybe some spectral analysis of $M$ gives us nice asymptotic info.