I recently ran across an article by Katherine Stange [1] on Lehmer’s factoring stencils [2]. These stencils were the basis of an effective method for factoring moderately large numbers before the advent of electronic computers.
This post will describe the stencils and simulate their use with a Python script.
Misconceptions
When I started reading [1] I had three misconceptions that slowed down my understanding of the article. I’ll address these first in case any of you come to this article with the same unhelpful expectations.
First, when I saw something about using stencils for factoring I thought they would be something like a Sieve of Aritosthenes, stencils with multiples of 2, 3, 5, etc. cut out. That is not what’s going on; Lehmer’s method is more sophisticated than that.
Second, related to the first, I thought that the factoring method would involve placing stencils on top of a large grid of numbers that included the number you wanted to factor. That is also not the case. The stencils can be used to factor nine-digit numbers, and a sheet of over a billion numbers would not be practical.
Third, I thought there might be some geometric significance to the position of the holes in the circular stencils. There isn’t. The stencils were circular for convenience.
How the stencils worked
Lehmer made a set of 295 stencils. Katherine Stange has put a set of SVG files for such stencils on her Github repo. The image below is the stencil corresponding to the number 42.
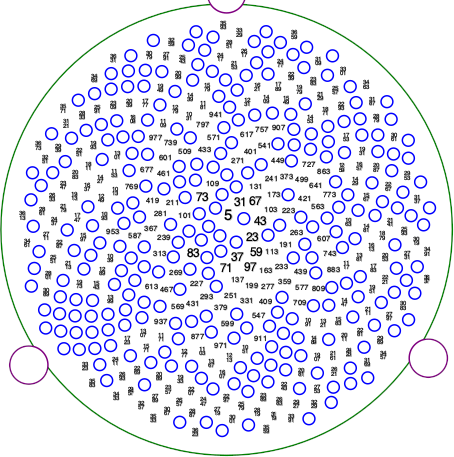
I want focus on how the stencils work, not why they work.
To factor a number N, you would first find a handful of numbers X1, X2, X3, … Xk, related to N, numbers that are fairly easy to compute by hand. Then you would stack the stencils corresponding to the Xi and hold the stack up to the light. If you could see light through a hole, the prime number labeling that hole would probably be a prime factor of N.
When I say the number would probably be prime, the probability would be on the order of 2−k. This explains why more stencils are better, but also why you don’t need that many stencils.
Once you found a probable prime factor, you would test it by long division, and then you know with certainty whether the number is a factor.
What is each stencil?
So what are these Xi and what are the holes in them?
The Xi are quadratic residues mod N, i.e. numbers such that
Xi = x² mod N
has a solution. This would have required some hand calculation, but not nearly as much calculation as trying to factor N unaided. A couple algorithms for finding quadratic residues are described in this video and in this PDF by Katherine Stange.
NB: The hard part isn’t finding quadratic residues mod N; you could do that by squaring random integers mod N. The hard part is finding quadratic residues that correspond to your set of available stencils.
The holes in the stencil correspond to the prime numbers up to 48593. Disk X has a hole for prime p if X is a quadratic residue mod X. If X is a quadratic residue mod p and mod N, there’s a 50-50 chance p divides N.
The number 48593 is the 4999th prime, so there are locations on each disk corresponding to 4999 primes. Lehmer arranged these locations in a spiral, but they could have been laid out in a grid or any other pattern.
Python simulation
See the Github repo referenced above for Python code to make the SVG files for the physical stencils. The Python code below simulates the operation of the stencils, not their geometry. I wrote the code to be illustrative, not to be practical efficient code for factoring integers.
First, here’s code to make our stencils. Here a 1 corresponds to a hole.
from sympy import primerange, legendre_symbol
from numpy import array
primes = array([p for p in primerange(3, 48594)])
def stencil(x):
# stencil has a 1 in position k if x is a quadratic residue
# modulo the kth odd prime and a 0 otherwise
return array([1 if legendre_symbol(x, p) == 1 else 0 for p in primes])
Next we pick an N and a few small quadratic residues mod N.
N = 19972009 x = [2, 103, 203, 206, 313, 238, 255, 421]
Multiplying the stencils together produces a 1 where every stencil has a hole.
mask = stencil(x[0])
for i in range(1, len(x)):
mask *= stencil(x[i])
ps = mask*primes
print(ps[ps != 0])
This prints the following:
[ 97 743 977 1913 1999 2287 4201 8111 13217 15241 15919 16759 17863 20201 21023 27487 27647 31657 32839 32993 34231 34513 34537 34759 38729 41057 41863 41999 42767 43721 45281 45319 47977]
We test whether 97 is a factor, and we get lucky: N = 97 × 205897.
Next we see if 205897 is divisible by 743, 977, 1913, 1999, …. The first three don’t work, but 1999 does: 205897 = 1999 × 103. We recognize 103 as a prime, and so we’re done:
19972009 = 97 × 103 × 1999.
Related posts
- Conway’s mental factoring method
- Factored random numbers
- Numbers don’t typically have many prime factors
[1] The Ingenious Physical Factoring Devices of D. N. Lehmer. Math Horizons. Volume 30 Issue 2. November 2022.
[2] D. N. Lehmer and his son D. H. Lehmer were both number theorists. I’ve referred to the later several times on the blog, most recently here. I also cited Katherine Stange a couple weeks ago.