Apollonius of Perga (c. 262 BC – c. 190 BC) discovered a theorem that generalizes the Pythagorean theorem but isn’t nearly as well known.
Let ABC be a general triangle, and let D be the midpoint of the segment AB. Let a be the length of the side opposite A and b the length of the side opposite B. Let m be the length of AD and h the length of the mediant, the line CD.
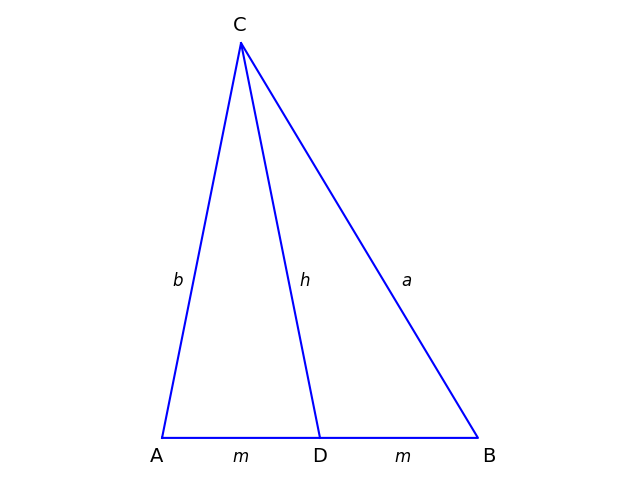
Apollonius’s theorem says
a² + b² = 2(m² + h²).
To see that this is a generalization of the Pythagorean theorem, apply Apollonius’ theorem to an isosceles triangle. Now a = b and ACD is a right triangle.
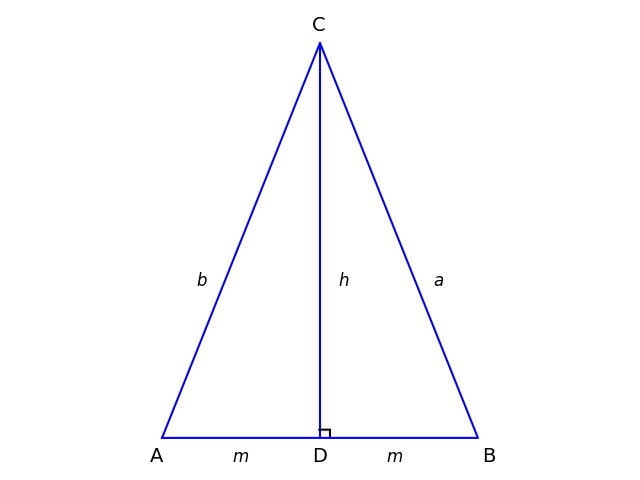
Apollonius’ theorem says
2b² = 2m² + 2h²
which is the Pythagorean theorem applied to ACD with each term doubled.
It’s actually a generalization of Pythagoras in two different ways. As well as the one shown here, you can take the original right triangle and draw the mediant line from the right-angled vertex. Since a right-angled triangle can be inscribed in a circle, we have h=m=c/2 and so Apollonius says a^2 + b^2 = 2(c^2/4+c^2/4) = c^2.