As I’ve written about several times lately, the Smith chart is the image of a rectangular grid in the right half-plane under the function
f(z) = (z − 1)/(z + 1).
What would the image of a grid in the left half-plane look like?
For starters, since f maps the right half-plane to the interior of the unit circle, it must map the left-half plane to the exterior of the unit circle.
As we said before, the function f is a Möbius transformation, and so it takes generalized circles, i.e. either a circle or a line, to generalized circles. So the grid lines in the left half-plane are either mapped to lines or circles. Which is it?
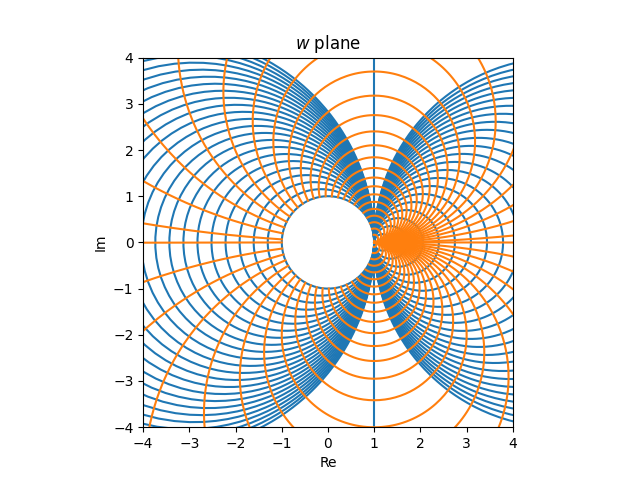
The function f has a singularity at −1 and so the image of any line (or circle) through z = −1 is unbounded, i.e. a line, not a circle. Any line not passing through −1 has a bounded image, which must be a circle.
The line Re(z) = −1 in the z plane is mapped to the line Re(w) = 1 in the w plane. Otherwise a vertical line crossing the real axis at x is mapped to a circle passing through w = (x − 1)/(x + 1). The circle also passes through w = 1 because f(∞) = 1. The circle is symmetric about the real axis, and so this is enough information to uniquely determine the circle.
Note that (x − 1)/(x + 1) > 1 when x < −1 and so vertical lines with real part less than −1 are mapped to circles to the right of w = 1. When −1 < x < 0, vertical lines are mapped to circles to the left of w = 1.
The images of horizontal lines we’ve looked at before. These are all circles passing through w = 1 and tangent to the circles that are images of vertical lines. But this time instead of taking the portion of the circles inside the unit circle, we take the portion outside the unit circle.
And without further ado, we present the anti-Smith chart, the image of a grid in the left half plane.