Spherical geometry
In spherical geometry, the interior angles of a triangle add up to more than π. And in fact you can determine the area of a spherical triangle by how much the angle sum exceeds π. On a sphere of radius 1, the area equals the triangle excess
Area = E = interior angle sum − π.
Small triangles have interior angle sum near π. But you could, for example, have a triangle with three right angles: put a vertex on the north pole and two vertices on the equator 90° longitude apart.
Hyperbolic geometry
In hyperbolic geometry, the sum of the interior angles of a triangle is always less than π. In a space with curvature −1, the area equals the triangle defect, the difference between π and the angle sum.
Area = D = π − interior angle sum.
Again small triangles have an interior angle sum near π. Both spherical and hyperbolic geometry are locally Euclidean.
The interior angle sum can be any value less than π, and so as the angle sum goes to 0, the triangle defect, and hence the area, goes to π.
The figure below has interior angle sum 0 and area π in hyperbolic geometry.
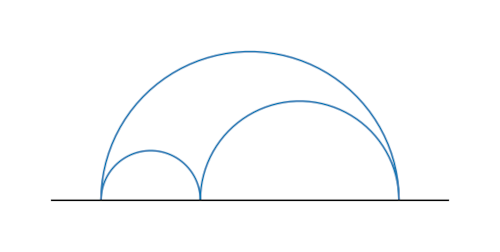
Strictly speaking this is an improper triangle because the three hyperbolic lines (i.e. half circles) don’t intersect within the hyperbolic plane per se but at ideal points on the real axis. But you could come as close to this triangle as you like, staying within the hyperbolic plane.
Note that the radii of the (Euclidean) half circles doesn’t change the area. Any three semicricles that intersect on the real line as above make a triangle with the same area.